Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-25T20:38:22.697Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation Algorithm and FPT Algorithm for Connected-k-Subgraph Cover on Minor-Free Graphs

Published online by Cambridge University Press:  10 January 2024

Pengcheng Liu ,
Zhao Zhang Open the ORCID record for Zhao Zhang [Opens in a new window] ,
Yingli Ran  and
Xiaohui Huang
Pengcheng Liu
Affiliation:
College of Computer Science and Artificial Intelligence, Wenzhou University,Wenzhou, Zhejiang, 325035, China
Zhao Zhang*
Affiliation:
School of Mathematical Sciences, Zhejiang Normal University, Jinhua, Zhejiang, 321004, China
Yingli Ran
Affiliation:
School of Mathematical Sciences, Zhejiang Normal University, Jinhua, Zhejiang, 321004, China
Xiaohui Huang
Affiliation:
School of Mathematical Sciences, Zhejiang Normal University, Jinhua, Zhejiang, 321004, China
*
Corresponding author: Zhao Zhang; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a graph G, the minimum Connected-k-Subgraph Cover problem (MinCkSC) is to find a minimum vertex subset C of G such that every connected subgraph of G on k vertices has at least one vertex in C. If furthermore the subgraph of G induced by C is connected, then the problem is denoted as MinCkSC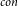$_{con}$. In this paper, we first present a PTAS for MinCkSC on an H-minor-free graph, where H is a graph with a constant number of vertices. Then, we design an 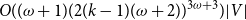$O((\omega+1)(2(k-1)(\omega+2))^{3\omega+3})|V|$-time FPT algorithm for MinCkSC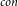$_{con}$ on a graph with treewidth 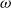$\omega$, based on which we further design an 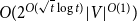$O(2^{O(\sqrt{t}\log t)}|V|^{O(1)})$ time subexponential FPT algorithm for MinCkSC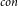$_{con}$ on an H-minor-free graph, where t is an upper bound of solution size.

Keywords

Connected-k-subgraph coverapproximation algorithmlocal searchminor-free graphPTASFPT
Type
Special Issue: TAMC 2022
Information
Mathematical Structures in Computer Science , Volume 34 , Special Issue 3: Theory and Applications of Models of Computation , March 2024 , pp. 180 - 192
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

*

This research is supported in part by National Natural Science Foundation of China (U20A2068, 11771013), Zhejiang Provincial Natural Science Foundation of China (LD19A010001).

References

Alon, N., Seymour, P. D. and Thomas, R. (1990). A separator theorem for nonplanar graphs. Journal of the American Mathematical Society 3 (4) 801–808.CrossRefGoogle Scholar
Bai, Z., Tu, J. and Shi, Y. (2019). An improved algorithm for the vertex cover P3 problem on graphs of bounded treewidth. Discrete Mathematics and Theoretical Computer Science 21 (4) #17.Google Scholar
Bar-Yehuda, R. and Even, S. (1981). A linear time approximation algorithm for the weighted vertex cover problem. Journal of Algorithms 2 198–203.CrossRefGoogle Scholar
Bar-Yehuda, R., Censor-Hillel, K.and Schwartzman, G. (2017). A distributed (2+ε)-approximation for vertex cover in $O(\log \Delta/ \varepsilon \log \log \Delta)$ rounds. Journal of the ACM 64 (3) #23 1-11.CrossRefGoogle Scholar
Bodlaender, H.L. (1996). A linear-time algorithm for finding tree-decompositions of small treewidth. SIAM Journal on Computing 25 (6) 1305–1317.CrossRefGoogle Scholar
Brešar, B., Kardoš, F., Katrenič, J.and Semanišin, G. (2011). Minimum k-path vertex cover. Discrete Applied Mathematics 159 (12) 1189–1195.CrossRefGoogle Scholar
Cabello, S. and Gajser, D. (2015). Simple PTAS’s for families of graphs excluding a minor. Discrete Applied Mathematics 189 41–48.CrossRefGoogle Scholar
Cai, L. (1996). Fixed-parameter tractability of graph modification problems for hereditary properties. Information Processing Letters 58 (4) 171–176.CrossRefGoogle Scholar
Cai, S., Li, Y., Hou, W. and Wang, H. (2019). Towards faster local search for minimum weight vertex cover on massive graphs. Information Sciences 3 (471) 64–79.CrossRefGoogle Scholar
Červený, R. and Suchý, O. (2019). Faster FPT algorithm for 5-path vertex cover. In: Proceeding of 44th International Symposium on Mathematical Foundations of Computer Science, MFCS 2019, vol. 138, pp. 32:1-32:13.Google Scholar
Chang, M.S., Chen, L.H., Hung, L.J., Rossmanith, P. and Su, P.C. (2016). Fixed-parameter algorithms for vertex cover P3 . Discrete Optimization 19 (471) 12–22.CrossRefGoogle Scholar
Chen, J., Kanj, I.A. and Xia, G. (2010). Improved upper bounds for vertex cover. Theoretical Computer Science 411 (40-42) 3736–3756.CrossRefGoogle Scholar
Cygan, M. (2012). Deterministic parameterized connected vertex cover. In : Proceedings of 13th Scandinavian Workshop on Algorithm Theory, SWAT 2012, in: LNCS, vol. 7357, pp. 95-106.CrossRefGoogle Scholar
Demaine, E.D.and Hajiaghayi, M.(2008). Linearity of grid minors in treewidth with applications through bidimensionality. Combinatorica 28 (1) 19–36.CrossRefGoogle Scholar
Diestel, R. (2005). Graph theory. 3rd edn, Springer, Heidelberg.Google Scholar
Gupta, A., Lee, E., Li, J., Manurangsi, P. (2019). Losing tree-width by separating subsets. In: Proceedings of the 30th Annual ACM-SIAM Symposium on Discrete Algorithms, SODA2019, pp. 1731-1749.Google Scholar
Guruswami, V. and Lee, E. (2017). Inapproximability of H-transversal/packing. SIAM Journal on Discrete Mathematics 31 (3) 1552–1571.CrossRefGoogle Scholar
Hochbaum, D.S. (1982). Approximation algorithms for the set covering and vertex cover problems. SIAM Journal on Computing 11 (3) 555–556.CrossRefGoogle Scholar
Kardoš, F., Katrenič, J.and Schiermeyer, I. (2011). On computing the minimum 3-path vertex cover and dissociation number of graphs. Theoretical Computer Science 412 (50) 7009–7017.CrossRefGoogle Scholar
Katrenič, J. (2016). A faster FPT algorithm for 3-path vertex cover. Information Processing Letters 116 (4) 273–278.CrossRefGoogle Scholar
Khot, S., Minzer, D.and Safra, M. (2018). Pseudorandom sets in grassmann graph have near-perfect expansion. In: 2018 IEEE 59th Annual Symposium on Foundations of Computer Science, FOCS2018, pp. 592-601.Google Scholar
Kloks, T. (1994). Treewidth: computations and approximations. Springer, Heidelberg.CrossRefGoogle Scholar
Le, H.and Zheng, B. (2020). Local search is a PTAS for feedback vertex set in minor-free graphs. Theoretical Computer Science 838 17–24.CrossRefGoogle Scholar
Lee, E.(2017). Partitioning a graph into small pieces with applications to path transversal. In: Proceedings of the 28th Annual ACM-SIAM Symposium on Discrete Algorithms, SODA2017, pp. 1546-1558.CrossRefGoogle Scholar
Li, X., Zhang, Z., Huang, X.(2016). Approximation algorithms for minimum (weight) connected k-path vertex cover. Discrete Applied Mathematics 205 101–108.CrossRefGoogle Scholar
Li, X., Shi, Y., Huang, X. (2018). PTAS for $\mathcal H$ -free node deletion problems in disk graphs. Discrete Applied Mathematics 239 119–124.CrossRefGoogle Scholar
Liu, P., Zhang, Z., Huang, X. (2020). Approximation algorithm for minimum weight connected-k-subgraph cover. Theoretical Computer Science 838 160–167.CrossRefGoogle Scholar
Novotný, M.(2010). Design and analysis of a generalized canvas protocol. In : Proceedings of 4th Information Security Theory and Practices: Security and Privacy of Pervasive Systems and Smart Devices, WISTP 2010, in: LNCS, vol. 6033, pp. 106C121.Google Scholar
Pourhassan, M., Shi, F. and Neumann, F. (2019). Parameterized analysis of multiobjective evolutionary algorithms and the weighted vertex cover problem. Evolutionary Computation 27 (4) 559–575.CrossRefGoogle ScholarPubMed
Ran, Y., Zhang, Z., Huang, X., Li, X. and Du, D. (2019). Approximation algorithms for minimum weight connected 3-path vertex cover. Applied Mathematics and Computation 347 723–733.CrossRefGoogle Scholar
Tsur, D. (2019). Parameterized algorithm for 3-path vertex vover. Theoretical Computer Science 783 1–8.CrossRefGoogle Scholar
Tsur, D. (2021). An $O^*(2.619^k)$ algorithm for 4-path vertex cover. Discrete Applied Mathematics 291 1–14.CrossRefGoogle Scholar
Tsur, D. (2019). l-path vertex cover is easier than l-hitting set for small l. ArXiv Preprint ArXiv:1906.10523.Google Scholar
Tu, J. (2015). A fixed-parameter algorithm for the vertex cover P3 problem. Information Processing Letters 115 96–99.CrossRefGoogle Scholar
Tu, J. and Jin, Z. (2016). An FPT algorithm for the vertex cover P4 problem. Discrete Applied Mathematics 200 186–190.CrossRefGoogle Scholar
Tu, J. and Zhou, W. (2011). A factor 2 approximation algorithm for the vertex cover P3 problem. Information Processing Letters 111 683–686.CrossRefGoogle Scholar
Tu, J. and Zhou, W. (2011). A primal-dual approximation algorithm for the vertex cover P3 problem. Theoretical Computer Science 412 7044–7048.CrossRefGoogle Scholar
Xiao, M. and Kou, S. (2017). Exact algorithms for the maximum dissociation set and minimum 3-path vertex cover problems. Theoretical Computer Science 657 86–97.CrossRefGoogle Scholar
Zhang, A., Chen, Y., Chen, Z.and Lin, G.H. (2018). Improved approximation algorithms for path vertex covers in regular graphs. ArXiv Preprint ArXiv: 1811.01162v1.Google Scholar
Zhang, Y., Shi, Y.S.and Zhang, Z.(2014). Approximation algorithm for the minimum weight connected k-subgraph cover problem. Theoretical Computer Science 535 54–58.CrossRefGoogle Scholar
Zhang, Z., Li, X., Shi, Y., Nie, H. and Zhu, Y. (2017). PTAS for minimum k-path vertex cover in ball graph. Information Processing Letters 119 9–13.CrossRefGoogle Scholar