No CrossRef data available.
 $^{\boldsymbol\omega}$
$^{\boldsymbol\omega}$Published online by Cambridge University Press: 17 April 2023
Werner’s set-theoretical model is one of the simplest models of CIC. It combines a functional view of predicative universes with a collapsed view of the impredicative sort “
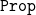 ${\tt Prop}$
”. However, this model of
${\tt Prop}$
”. However, this model of
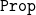 ${\tt Prop}$
is so coarse that the principle of excluded middle
${\tt Prop}$
is so coarse that the principle of excluded middle
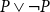 $P \lor \neg P$
holds. Following our previous work, we interpret
$P \lor \neg P$
holds. Following our previous work, we interpret
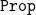 ${\tt Prop}$
into a topological space (a special case of Heyting algebra) to make the model more intuitionistic without sacrificing simplicity. We improve on that work by providing a full interpretation of dependent product types, using Alexandroff spaces. We also extend our approach to inductive types by adding support for
${\tt Prop}$
into a topological space (a special case of Heyting algebra) to make the model more intuitionistic without sacrificing simplicity. We improve on that work by providing a full interpretation of dependent product types, using Alexandroff spaces. We also extend our approach to inductive types by adding support for
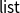 ${\mathsf{list}}$
s.
${\mathsf{list}}$
s.