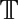 $\mathbb{T}$ω
$\mathbb{T}$ωPublished online by Cambridge University Press: 22 May 2015
In 1978, G. Plotkin noticed that 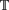 $\mathbb{T}$ω, the cartesian product of ω copies of the three element flat domain of Booleans, is a universal domain, where ‘universal’ means that the retracts of
$\mathbb{T}$ω, the cartesian product of ω copies of the three element flat domain of Booleans, is a universal domain, where ‘universal’ means that the retracts of 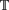 $\mathbb{T}$ω for Scott's continuous semantics are exactly all the ωCC-domains, which with Scott continuous functions form a cartesian closed category. As usual, ‘ω’ is for ‘countably based,’ and here ‘CC’ is for ‘conditionally complete,’ which essentially means that any subset which is pairwise bounded has a least upper bound. Since
$\mathbb{T}$ω for Scott's continuous semantics are exactly all the ωCC-domains, which with Scott continuous functions form a cartesian closed category. As usual, ‘ω’ is for ‘countably based,’ and here ‘CC’ is for ‘conditionally complete,’ which essentially means that any subset which is pairwise bounded has a least upper bound. Since 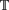 $\mathbb{T}$ω is also an ωDI-domain (an important structure in stable domain theory), the following problem arises naturally: is there a cartesian closed category C of domains with stable functions such that
$\mathbb{T}$ω is also an ωDI-domain (an important structure in stable domain theory), the following problem arises naturally: is there a cartesian closed category C of domains with stable functions such that 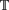 $\mathbb{T}$ω, or a related structure, is universal in C for Berry’s stable semantics? The aim of this paper is to answer this question. We first investigate the properties of stable retracts. We introduce a new class of domains called conditionally complete DI-domains (CCDI-domain for short) and show that, (1)
$\mathbb{T}$ω, or a related structure, is universal in C for Berry’s stable semantics? The aim of this paper is to answer this question. We first investigate the properties of stable retracts. We introduce a new class of domains called conditionally complete DI-domains (CCDI-domain for short) and show that, (1) 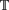 $\mathbb{T}$ω is an ωCCDI-domain and the category of CCDI-domains (resp. ωCCDI-domains) with stable functions is cartesian closed; (2) [
$\mathbb{T}$ω is an ωCCDI-domain and the category of CCDI-domains (resp. ωCCDI-domains) with stable functions is cartesian closed; (2) [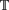 $\mathbb{T}$ω →st
$\mathbb{T}$ω →st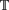 $\mathbb{T}$ω] is a stable universal domain in the sense that every ωCCDI-domain is a stable retract of [
$\mathbb{T}$ω] is a stable universal domain in the sense that every ωCCDI-domain is a stable retract of [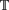 $\mathbb{T}$ω → st
$\mathbb{T}$ω → st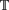 $\mathbb{T}$ω], where [
$\mathbb{T}$ω], where [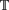 $\mathbb{T}$ω → st
$\mathbb{T}$ω → st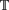 $\mathbb{T}$ω] is the stable function space of
$\mathbb{T}$ω] is the stable function space of 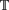 $\mathbb{T}$ω; (3) in particular, [
$\mathbb{T}$ω; (3) in particular, [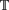 $\mathbb{T}$ω → st
$\mathbb{T}$ω → st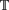 $\mathbb{T}$ω] is not a stable retract of
$\mathbb{T}$ω] is not a stable retract of 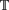 $\mathbb{T}$ω and hence
$\mathbb{T}$ω and hence 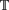 $\mathbb{T}$ω is not universal for Berry’s stable semantics. We remark that this paper is a completion and correction of our earlier report in the Proceedings of the 6th International Symposium on Domain Theory and Its Applications (ISDT2013).
$\mathbb{T}$ω is not universal for Berry’s stable semantics. We remark that this paper is a completion and correction of our earlier report in the Proceedings of the 6th International Symposium on Domain Theory and Its Applications (ISDT2013).