Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T21:37:49.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Rewriting with generalized nominal unification

Published online by Cambridge University Press:  22 May 2020

Yunus Kutz  and
Manfred Schmidt-Schauß Open the ORCID record for Manfred Schmidt-Schauß [Opens in a new window]
Yunus Kutz
Affiliation:
Goethe-University, Frankfurt am Main, Germany
Manfred Schmidt-Schauß*
Affiliation:
Goethe-University, Frankfurt am Main, Germany
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider matching, rewriting, critical pairs and the Knuth–Bendix confluence test on rewrite rules in a nominal setting extended by atom-variables. We utilize atom-variables instead of atoms to formulate and rewrite rules on constrained expressions, which is an improvement of expressiveness over previous approaches. Nominal unification and nominal matching are correspondingly extended. Rewriting is performed using nominal matching, and computing critical pairs is done using nominal unification. We determine the complexity of several problems in a quantified freshness logic. In particular we show that nominal matching is 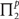$$\prod _2^p$$ -complete. We prove that the adapted Knuth–Bendix confluence test is applicable to a nominal rewrite system with atom-variables, and thus that there is a decidable test whether confluence of the ground instance of the abstract rewrite system holds. We apply the nominal Knuth–Bendix confluence criterion to the theory of monads and compute a convergent nominal rewrite system modulo alpha-equivalence.

Keywords

Nominal unificationnominal rewritingKnuth–Bendix confluence criterionatom-variablesconfluence
Type
Paper
Information
Mathematical Structures in Computer Science , Volume 30 , Special Issue 6: Special Issue: Unification , June 2020 , pp. 710 - 735
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Manfred Schmidt-Schauß is supported by the Deutsche Forschungsgemeinschaft (DFG) under grant SCHM 986/11-1.

References

Aoto, T. and Kikuchi, K. (2016). Nominal confluence tool. In: International Joint Conference on Automated Reasoning, Springer, 173–182.10.1007/978-3-319-40229-1_12CrossRefGoogle Scholar
Ariola, Z. M., Felleisen, M., Maraist, J., Odersky, M. and Wadler, P. (1995). A call-by-need lambda calculus. In: POPL 1995, ACM Press, 233–246.CrossRefGoogle Scholar
Ayala-Rincón, M., de Carvalho-Segundo, W., Fernández, M. and Nantes-Sobrinho, D. (2019a). A formalisation of nominal c-matching through unification with protected variables. Electronic Notes in Theoretical Computer Science 344 47–65.10.1016/j.entcs.2019.07.004CrossRefGoogle Scholar
Ayala-Rincón, M., Fernández, M., Gabbay, M. J. and Rocha-Oliveira, A. C. (2016). Checking overlaps of nominal rewriting rules. Electronic Notes in Theoretical Computer Science 323 39–56.CrossRefGoogle Scholar
Ayala-Rincón, M., Fernández, M., Silva, G. F. and Nantes-Sobrinho, D. (2019b). A certified functional nominal c-unification algorithm. In: Pre-Proceedings of the 29th International Symposium Logic-Based Program Synthesis and Transformation (LOPSTR). CrossRefGoogle Scholar
Calvès, C. and Fernández, M. (2008). A polynomial nominal unification algorithm. Theoretical Computer Science 403 (2-3) 285–306.CrossRefGoogle Scholar
Cheney, J. (2004). Nominal Logic Programming. PhD thesis, Cornell University.Google Scholar
Cheney, J. (2010). Equivariant unification. Journal of Automated Reasoning 45 (3) 267–300.CrossRefGoogle Scholar
Fernández, M. and Gabbay, M. J. (2007). Nominal rewriting. Information and Computation 205 (6) 917–965.10.1016/j.ic.2006.12.002CrossRefGoogle Scholar
Fernández, M. and Gabbay, M. J. (2010). Closed nominal rewriting and efficiently computable nominal algebra equality. In: Crary, K. and Miculan, M. (eds.) Proceedings 5th International Workshop on Logical Frameworks and Meta-languages: Theory and Practice, LFMTP 2010, Edinburgh, UK, 14th July 2010, EPTCS, vol. 34, 37–51.CrossRefGoogle Scholar
Fernández, M., Gabbay, M. J. and Mackie, I. (2004). Nominal rewriting systems. In: Proceedings of the 6th ACM SIGPLAN International Conference on Principles and Practice of Declarative Programming, PPDP 2004, ACM, 108–119.10.1145/1013963.1013978CrossRefGoogle Scholar
Fernández, M. and Rubio, A. (2012). Nominal completion for rewrite systems with binders. In Czumaj, A., Mehlhorn, K., Pitts, A. M. and Wattenhofer, R. (eds.) Proceedings 39th ICALP Part II, LNCS, vol. 7392, Springer, 201–213.10.1007/978-3-642-31585-5_21CrossRefGoogle Scholar
Hamana, M. (2017). How to prove your calculus is decidable: practical applications of second-order algebraic theories and computation. Proceedings of the ACM on Programming Languages 1 (ICFP) 22:1–22:28.Google Scholar
Haskell-community (2019). Haskell Main Website. www.haskell.org.Google Scholar
Kikuchi, K., Aoto, T., and Toyama, Y. (2017). Parallel closure theorem for left-linear nominal rewriting systems. In: International Symposium on Frontiers of Combining Systems, Springer, 115–131.10.1007/978-3-319-66167-4_7CrossRefGoogle Scholar
Knuth, D. and Bendix, P. B. (1970). Simple word problems in universal algebra. In: Leech, J. (ed.) Computational Problems in Abstract Algebra, Pergamon Press, 263–297.Google Scholar
Levy, J. and Villaret, M. (2010). An efficient nominal unification algorithm. In: Lynch, C. (ed.) Proceedings of 21st RTA, LIPIcs, vol. 6, Schloss Dagstuhl, 209–226.Google Scholar
Papadimitriou, C. (1994). Computational Complexity. Addison-Wesley.Google Scholar
Peyton Jones, S. L. (2003). Haskell 98 Language and Libraries: The Revised Report. Cambridge University Press. www.haskell.org.Google Scholar
Peyton Jones, S. L., Gordon, A. and Finne, S. (1996). Concurrent Haskell. In Proceedings of 23rd ACM POPL 1996, ACM, 295–308.Google Scholar
Pitts, A. (2016). Nominal techniques. ACM SIGLOG News 3 (1) 57–72.10.1145/2893582.2893594CrossRefGoogle Scholar
Pitts, A. M. (2013). Nominal Sets: Names and Symmetry in Computer Science. Cambridge University Press.CrossRefGoogle Scholar
Sabel, D. and Schmidt-Schauß, M. (2011). A contextual semantics for concurrent Haskell with futures. In: Schneider-Kamp, P. and Hanus, M. (eds.) Proceedings of 13th ACM PPDP 2011, ACM, 101–112.10.1145/2003476.2003492CrossRefGoogle Scholar
Sabel, D. and Schmidt-Schauß, M. (2012). Conservative concurrency in Haskell. In: LICS 2012, IEEE, 561–570.10.1109/LICS.2012.66CrossRefGoogle Scholar
Schmidt-Schauß, M. and Sabel, D. (2018). Nominal unification with atom and context variables. In: Kirchner, H. (ed.) 3rd International Conference on Formal Structures for Computation and Deduction, FSCD 2018, July 9–12, 2018, Oxford, UK, LIPIcs, vol. 108, Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik, 28:1–28:20.Google Scholar
Schmidt-Schauß, M., Sabel, D. and Kutz, Y. D. K. (2019). Nominal unification with atom-variables. Journal of Symbolic Computation 90 42–64.CrossRefGoogle Scholar
Suzuki, T., Kikuchi, K., Aoto, T. and Toyama, Y. (2015). Confluence of orthogonal nominal rewriting systems revisited. In: 26th International Conference on Rewriting Techniques and Applications (RTA 2015). Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik.Google Scholar
Suzuki, T., Kikuchi, K., Aoto, T. and Toyama, Y. (2016). Critical pair analysis in nominal rewriting. In: SCSS, 156–168.Google Scholar
Urban, C. (2008). Nominal techniques in Isabelle/HOL. Journal of Automated Reasoning 40 (4) 327–356.10.1007/s10817-008-9097-2CrossRefGoogle Scholar
Urban, C. and Kaliszyk, C. (2012). General bindings and alpha-equivalence in nominal Isabelle. Logical Methods in Computer Science 8 (2) 1–35.10.2168/LMCS-8(2:14)2012CrossRefGoogle Scholar
Urban, C., Pitts, A. M. and Gabbay, M. (2003). Nominal unification. In: 17th CSL, 12th EACSL, and 8th KGC, LNCS, vol. 2803, Springer, 513–527.CrossRefGoogle Scholar
Urban, C., Pitts, A. M. and Gabbay, M. J. (2004). Nominal unification. Theoretical Computer Science 323 (1–3) 473–497.10.1016/j.tcs.2004.06.016CrossRefGoogle Scholar
Wadler, P. (1995). Monads for functional programming. In: Jeuring, J. and Meijer, E. (eds.) Advanced Functional Programming, First International Spring School on Advanced Functional Programming Techniques, Båstad, Sweden, May 24-30, 1995, Tutorial Text, LNCS, vol. 925, Springer, 24–52.CrossRefGoogle Scholar