Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-09T05:37:26.615Z Has data issue: false hasContentIssue false
  • English
  • Français

Representing prefix and border tables: results on enumeration

Published online by Cambridge University Press:  22 May 2015

JULIEN CLÉMENT  and
LAURA GIAMBRUNO
JULIEN CLÉMENT
Affiliation:
Departement d'Informatique, Universite de Caen Basse-Normandie, Caen, France Email: [email protected], [email protected]
LAURA GIAMBRUNO
Affiliation:
Departement d'Informatique, Universite de Caen Basse-Normandie, Caen, France Email: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For some text algorithms, the real measure for the complexity analysis is not the string itself but its structure stored in its prefix table or equivalently border table. In this paper, we define the combinatorial class of prefix lists, namely a sequence of integers together with their size, and an injection ψ from the class of prefix tables to the class of prefix lists. We call a valid prefix list the image by ψ of a prefix table. In particular, we describe algorithms converting a prefix/border table to a prefix list and inverse linear algorithms from computing from a prefix list L = ψ(P) two words respectively in a minimal size alphabet and on a maximal size alphabet with P as prefix table. We then give a new upper bound on the number of prefix tables for strings of length n (on any alphabet) which is of order (1 + ϕ)n (with 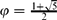$\varphi=\frac{1+\sqrt{5}}{2}$ the golden mean) and also present a corresponding lower bound.

Type
Paper
Information
Mathematical Structures in Computer Science , Volume 27 , Special Issue 2: Special Issue: XIV ICTCS , February 2017 , pp. 257 - 276
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bland, W., Kucherov, G. and Smyth, W. F. (2013). Prefix table construction and conversion. Lecture Notes in Computer Science (LNCS) 8288 41–53.CrossRefGoogle Scholar
Cartan, H. (1985). Théorie élémentaire des fonctions analytiques d'une ou plusieurs variables complexes, Hermann.Google Scholar
Clément, J., Crochemore, C. and Rindone, G. (2009). Reverse engineering prefix tables. In: Leibniz International Proceedings in Informatics (LIPIcs), volume 3, 289–300. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik.Google Scholar
Clément, J. and Giambruno, L. (2014). On the number of prefix and border tables. In: Proceedings of LATIN 2014: Theoretical Informatics. Lecture Notes in Computer Science (LNCS) 8392 442–453.Google Scholar
Crochemore, M., Hancart, C. and Lecroq, T. (2007). Algorithms on Strings, Cambridge University Press, Cambridge, UK.CrossRefGoogle Scholar
Duval, J.-P., Lecroq, T. and Lefebvre, A. (2005). Border array on bounded alphabet. Journal of Automata, Languages and Combinatorics 10 (1) 51–60.Google Scholar
Duval, J.-P., Lecroq, T. and Lefebvre, A. (2009). Efficient validation and construction of border arrays and validation of string matching automata. RAIRO-Theoretical Informatics and Applications 43 (2) 281–297.CrossRefGoogle Scholar
Flajolet, P. and Sedgewick, R. (2009). Analytic Combinatorics, Cambridge University Press, Cambridge, UK.CrossRefGoogle Scholar
Franek, F., Gao, S., Lu, W., Ryan, P. J., Smith, W. F., Sun, Y. and Yang, L. (2002). Verifying a border array in linear time. Journal on Combinatorial Mathematics and Combinatorial Computing 42 223–236.Google Scholar
Gusfield, D. (1997). Algorithms on Strings, Trees and Sequences: Computer Science and Computational Biology, Cambridge University Press, Cambridge, UK.CrossRefGoogle Scholar
Knuth, D. E. (1978). The average time for carry propagation. Indagationes Mathematicae 40 238–242.CrossRefGoogle Scholar
Moore, D., Smyth, W. F. and Miller, D. (1999). Counting distinct strings. Algorithmica 23 (1) 1–13.CrossRefGoogle Scholar