Article contents
Realizability interpretation of PA by iterated limiting PCA
Published online by Cambridge University Press: 11 March 2014
Abstract
For any partial combinatory algebra (PCA for short)  $\mathcal{A}$, the class of
$\mathcal{A}$, the class of  $\mathcal{A}$-representable partial functions from
$\mathcal{A}$-representable partial functions from 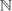 $\mathbb{N}$ to
$\mathbb{N}$ to  $\mathcal{A}$ quotiented by the filter of cofinite sets of
$\mathcal{A}$ quotiented by the filter of cofinite sets of 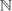 $\mathbb{N}$ is a PCA such that the representable partial functions are exactly the limiting partial functions of
$\mathbb{N}$ is a PCA such that the representable partial functions are exactly the limiting partial functions of  $\mathcal{A}$-representable partial functions (Akama 2004). The n-times iteration of this construction results in a PCA that represents any n-iterated limiting partial recursive function, and the inductive limit of the PCAs over all n is a PCA that represents any arithmetical partial function. Kleene's realizability interpretation over the former PCA interprets the logical principles of double negation elimination for Σ0n-formulae, and over the latter PCA, it interprets Peano's arithmetic (PA for short). A hierarchy of logical systems between Heyting's arithmetic (HA for short) and PA is used to discuss the prenex normal form theorem, relativised independence-of-premise schemes, and the statement ‘PA is an unbounded extension of HA’.
$\mathcal{A}$-representable partial functions (Akama 2004). The n-times iteration of this construction results in a PCA that represents any n-iterated limiting partial recursive function, and the inductive limit of the PCAs over all n is a PCA that represents any arithmetical partial function. Kleene's realizability interpretation over the former PCA interprets the logical principles of double negation elimination for Σ0n-formulae, and over the latter PCA, it interprets Peano's arithmetic (PA for short). A hierarchy of logical systems between Heyting's arithmetic (HA for short) and PA is used to discuss the prenex normal form theorem, relativised independence-of-premise schemes, and the statement ‘PA is an unbounded extension of HA’.
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2014
References
- 1
- Cited by


