Hostname: page-component-6bf8c574d5-m789k Total loading time: 0 Render date: 2025-03-08T00:27:51.815Z Has data issue: false hasContentIssue false
  • English
  • Français

The long exact sequence of homotopy n-groups

Published online by Cambridge University Press:  07 September 2023

Ulrik Buchholtz Open the ORCID record for Ulrik Buchholtz [Opens in a new window]  and
Egbert Rijke
Ulrik Buchholtz*
Affiliation:
Technische Universität Darmstadt, Fachbereich Mathematik, Schlossgartenstrasse 7, 64289 Darmstadt, Germany School of Computer Science, University of Nottingham, Jubilee Campus, Wollaton Road, Nottingham NG8 1BB, UK
Egbert Rijke
Affiliation:
University of Ljubljana, Fakulteta za matematiko in fiziko, Jadranska 19, 1000 Ljubljana, Slovenia
*
Corresponding author: Ulrik Buchholtz; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Working in homotopy type theory, we introduce the notion of n-exactness for a short sequence 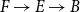$F\to E\to B$ of pointed types and show that any fiber sequence 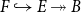$F\hookrightarrow E \twoheadrightarrow B$ of arbitrary types induces a short sequence

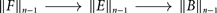
that is n-exact at 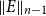$\| E\|_{n-1}$. We explain how the indexing makes sense when interpreted in terms of n-groups, and we compare our definition to the existing definitions of an exact sequence of n-groups for 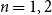$n=1,2$. As the main application, we obtain the long n-exact sequence of homotopy n-groups of a fiber sequence.

Keywords

Homotopy type theoryunivalent foundationshigher groupslong exact sequence
Type
Special Issue: Homotopy Type Theory 2019
Information
Mathematical Structures in Computer Science , Volume 33 , Special Issue 8: Homotopy Type Theory 2019 , September 2023 , pp. 679 - 687
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aldrovandi, E. and Noohi, B. (2009). Butterflies. I. Morphisms of 2-group stacks. Advances in Mathematics 221 (3) 687–773. http:10.1016/j.aim.2008.12.014.CrossRefGoogle Scholar
Buchholtz, U., van Doorn, F. and Rijke, E. (2018). Higher groups in homotopy type theory. In: Proceedings of the 33rd Annual ACM/IEEE Symposium on Logic in Computer Science, LICS’18, New York, NY, USA, ACM, 205–214. doi: 10.1145/3209108.3209150.CrossRefGoogle Scholar
Kasangian, S., Metere, G. and Vitale, E. M. (2011). The ziqqurath of exact sequences of n-groupoids. Cahiers de Topologie et Géométrie Différentielle Catégoriques 52 (1) 2–44. http://www.numdam.org/item/CTGDC_2011__52_1_2_0.Google Scholar
Licata, D. R. and Finster, E. (2014). Eilenberg-MacLane spaces in homotopy type theory. In: Proceedings of the Joint Meeting of the Twenty-Third EACSL Annual Conference on Computer Science Logic (CSL) and the Twenty-Ninth Annual ACM/IEEE Symposium on Logic in Computer Science (LICS), New York, ACM, Article No. 66, 10.Google Scholar
Lumsdaine, P. L. and Shulman, M. (2020). Semantics of higher inductive types. Mathematical Proceedings of the Cambridge Philosophical Society 169 (1) 159–208. doi: 10.1017/S030500411900015X.CrossRefGoogle Scholar
Lurie, J. (2009). Higher Topos Theory , Annals of Mathematics Studies, vol 170, Princeton, NJ: Princeton University Press, xviii+925. doi: 10.1515/9781400830558.Google Scholar
Rijke, E., Shulman, M. and Spitters, B. (2020). Modalities in homotopy type theory. Logical Methods in Computer Science 16 (1). doi: 10.23638/LMCS- 16(1:2)2020.Google Scholar
Shulman, M. (2019) All $(\infty,1)$ -toposes have strict univalent universes. arXiv:1904.07004.Google Scholar
Univalent Foundations Program (2013). Homotopy Type Theory: Univalent Foundations of Mathematics. Institute for Advanced Study: http://homotopytypetheory.org/book/.Google Scholar
Vitale, E. M. (2002). A Picard-Brauer exact sequence of categorical groups. In: 1–3 Special volume celebrating the 70th birthday of Professor Max Kelly, vol. 175, 383–408. doi: 10.1016/S0022-4049(02)00142-1.CrossRefGoogle Scholar
Voevodsky, V., Ahrens, B., Grayson, D. et al. (n.d). UniMath — a computer-checked library of univalent mathematics. http://UniMath.org.Google Scholar