Article contents
A domain-theoretic framework for robustness analysis of neural networks
Published online by Cambridge University Press: 23 May 2023
Abstract
A domain-theoretic framework is presented for validated robustness analysis of neural networks. First, global robustness of a general class of networks is analyzed. Then, using the fact that Edalat’s domain-theoretic L-derivative coincides with Clarke’s generalized gradient, the framework is extended for attack-agnostic local robustness analysis. The proposed framework is ideal for designing algorithms which are correct by construction. This claim is exemplified by developing a validated algorithm for estimation of Lipschitz constant of feedforward regressors. The completeness of the algorithm is proved over differentiable networks and also over general position
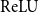 ${\mathrm{ReLU}}$
networks. Computability results are obtained within the framework of effectively given domains. Using the proposed domain model, differentiable and non-differentiable networks can be analyzed uniformly. The validated algorithm is implemented using arbitrary-precision interval arithmetic, and the results of some experiments are presented. The software implementation is truly validated, as it handles floating-point errors as well.
${\mathrm{ReLU}}$
networks. Computability results are obtained within the framework of effectively given domains. Using the proposed domain model, differentiable and non-differentiable networks can be analyzed uniformly. The validated algorithm is implemented using arbitrary-precision interval arithmetic, and the results of some experiments are presented. The software implementation is truly validated, as it handles floating-point errors as well.
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 2
- Cited by



