Published online by Cambridge University Press: 18 January 2016
In this paper, we treat the specification problem in Krivine classical realizability (Krivine 2009
Panoramas et synthèses
27), in the case of arithmetical formulæ. In the continuity of previous works from Miquel and the first author (Guillermo 2008
Jeux de réalisabilité en arithmétique classique, Ph.D. thesis, Université Paris 7; Guillermo and Miquel 2014
Mathematical Structures in Computer Science, Epub ahead of print), we characterize the universal realizers of a formula as being the winning strategies for a game (defined according to the formula). In the first sections, we recall the definition of classical realizability, as well as a few technical results. In Section 5, we introduce in more details the specification problem and the intuition of the game-theoretic point of view we adopt later. We first present a game
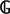 1, that we prove to be adequate and complete if the language contains no instructions ‘quote’ (Krivine 2003
Theoretical Computer Science
308 259–276), using interaction constants to do substitution over execution threads. We then show that as soon as the language contain ‘Quote,’ the game is no more complete, and present a second game
1, that we prove to be adequate and complete if the language contains no instructions ‘quote’ (Krivine 2003
Theoretical Computer Science
308 259–276), using interaction constants to do substitution over execution threads. We then show that as soon as the language contain ‘Quote,’ the game is no more complete, and present a second game
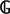 2 that is both adequate and complete in the general case. In the last Section, we draw attention to a model-theoretic point of view and use our specification result to show that arithmetical formulæ are absolute for realizability models.
2 that is both adequate and complete in the general case. In the last Section, we draw attention to a model-theoretic point of view and use our specification result to show that arithmetical formulæ are absolute for realizability models.