Published online by Cambridge University Press: 10 January 2022
It is well known that classical varieties of
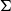 $\Sigma$
-algebras correspond bijectively to finitary monads on
$\Sigma$
-algebras correspond bijectively to finitary monads on
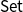 $\mathsf{Set}$
. We present an analogous result for varieties of ordered
$\mathsf{Set}$
. We present an analogous result for varieties of ordered
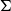 $\Sigma$
-algebras, that is, categories of algebras presented by inequations between
$\Sigma$
-algebras, that is, categories of algebras presented by inequations between
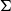 $\Sigma$
-terms. We prove that they correspond bijectively to strongly finitary monads on
$\Sigma$
-terms. We prove that they correspond bijectively to strongly finitary monads on
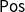 $\mathsf{Pos}$
. That is, those finitary monads which preserve reflexive coinserters. We deduce that strongly finitary monads have a coinserter presentation, analogous to the coequalizer presentation of finitary monads due to Kelly and Power. We also show that these monads are liftings of finitary monads on
$\mathsf{Pos}$
. That is, those finitary monads which preserve reflexive coinserters. We deduce that strongly finitary monads have a coinserter presentation, analogous to the coequalizer presentation of finitary monads due to Kelly and Power. We also show that these monads are liftings of finitary monads on
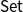 $\mathsf{Set}$
. Finally, varieties presented by equations are proved to correspond to extensions of finitary monads on
$\mathsf{Set}$
. Finally, varieties presented by equations are proved to correspond to extensions of finitary monads on
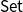 $\mathsf{Set}$
to strongly finitary monads on
$\mathsf{Set}$
to strongly finitary monads on
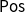 $\mathsf{Pos}$
.
$\mathsf{Pos}$
.
J. Adámek and M. Dostál acknowledge the support of the grant No. 19-0092S of the Czech Grant Agency.