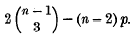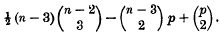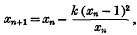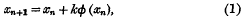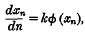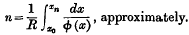Research Article
An integral equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 165-173
-
- Article
- Export citation
On the canonical curve of genus five
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 174-189
-
- Article
- Export citation
On some series of functions, (3)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 190-205
-
- Article
- Export citation
Note on the trisecants and quadrisecants of a space curve
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 206-208
-
- Article
- Export citation
Photo-electric absorption in hydrogen-like atoms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 209-218
-
- Article
- Export citation
On the theory of the recombination of ions in gases at high pressures
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 219-233
-
- Article
- Export citation
On the non-linear difference equation Δxn = kΦ (xn)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 234-243
-
- Article
- Export citation
A mathematical theory of natural and artificial selection. Part IX. Rapid selection
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 244-248
-
- Article
- Export citation
The energy exchanges between molecules
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 249-255
-
- Article
- Export citation
Front Matter
PSP volume 28 issue 2 Cover, Front matter and Corrigenda
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f3
-
- Article
- Export citation
Back Matter
PSP volume 28 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
- Export citation

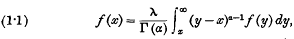
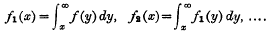
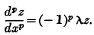
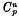 of order
of order