Research Article
Some points in βN
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 385-398
-
- Article
- Export citation
Non-singular models of specialized Weddle surfaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 399-418
-
- Article
- Export citation
Cliques in random graphs
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 419-427
-
- Article
- Export citation
On the duality of interaction models
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 429-436
-
- Article
- Export citation
A Fitting class construction
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 437-446
-
- Article
- Export citation
The supersolvable residual of an
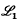 -group
-group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 447-450
-
- Article
- Export citation
Abstract length functions in groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 451-463
-
- Article
- Export citation
Banach algebras and absolutely summing operators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 465-473
-
- Article
- Export citation
Uniqueness of BSO
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 475-509
-
- Article
- Export citation
The case of the jumping critical point
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 511-520
-
- Article
- Export citation
Stochastic bounds for the single-server queue
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 521-525
-
- Article
- Export citation
A new derivation of the W.K.B. solution for the coupled equations of radio waves in the ionosphere
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 527-534
-
- Article
- Export citation
Modifications of Coulombic interactions by polarizable atoms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 535-539
-
- Article
- Export citation
Oblique slot blowing into a supersonic laminar boundary layer
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 541-554
-
- Article
- Export citation
On eigenstresses in a semi-infinite solid
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 555-562
-
- Article
- Export citation
Proceedings of meetings
Proceedings of the meetings held during the session 1975–76
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 563-569
-
- Article
- Export citation
Front matter
PSP volume 80 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 80 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b13
-
- Article
-
- You have access
- Export citation

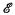 of order 32. This representation of
of order 32. This representation of 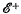 , of order 16, consisting of identity and the 15 products
, of order 16, consisting of identity and the 15 products 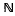 , the set of natural numbers, such that each edge occurs with probability
, the set of natural numbers, such that each edge occurs with probability 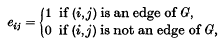
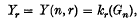
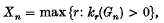
 -group
-group
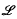 be the class of groups possessing a subgroup of index
be the class of groups possessing a subgroup of index 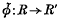 by
by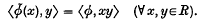
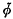 be
be