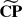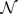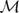Research Article
Summation of a random multiplicative function on numbers having few prime factors
-
- Published online by Cambridge University Press:
- 13 December 2010, pp. 193-214
-
- Article
- Export citation
Badly approximable numbers and Littlewood-type problems
-
- Published online by Cambridge University Press:
- 12 January 2011, pp. 215-226
-
- Article
- Export citation
Symmetric Auslander and Bass categories
-
- Published online by Cambridge University Press:
- 18 January 2011, pp. 227-240
-
- Article
- Export citation
Generalisations of the Euler adic
-
- Published online by Cambridge University Press:
- 22 October 2010, pp. 241-256
-
- Article
- Export citation
Irredundant families of subcubes
-
- Published online by Cambridge University Press:
- 12 January 2011, pp. 257-272
-
- Article
- Export citation
Stiefel–Whitney numbers for singular varieties
-
- Published online by Cambridge University Press:
- 18 January 2011, pp. 273-289
-
- Article
- Export citation
Product structures for Legendrian contact homology
-
- Published online by Cambridge University Press:
- 02 December 2010, pp. 291-311
-
- Article
- Export citation
A minimal volume arithmetic cusped complex hyperbolic orbifold
-
- Published online by Cambridge University Press:
- 08 October 2010, pp. 313-342
-
- Article
- Export citation
Non-real zeros of derivatives of real meromorphic functions of infinite order
-
- Published online by Cambridge University Press:
- 20 September 2010, pp. 343-351
-
- Article
- Export citation
On statistical attractors and the convergence of time averages
-
- Published online by Cambridge University Press:
- 12 January 2011, pp. 353-365
-
- Article
- Export citation
Inflation of strongly connected networks
-
- Published online by Cambridge University Press:
- 12 January 2011, pp. 367-384
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 150 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 01 February 2011, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PSP volume 150 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 01 February 2011, pp. b1-b2
-
- Article
-
- You have access
- Export citation


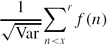
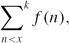
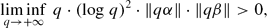
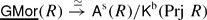
 (which is attained by the family of all
(which is attained by the family of all 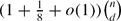 .
.