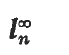1. The results. Let l be an odd prime, r ≥ 1, and let

be the quaternion group of order 4lr, as given by generators and relations. Throughout N is a tamely ramified normal number field with Galois group Gal (N/Q) = H (a ‘quaternion field’), and its ring of integers. We are interested in the structure of as a module over the integral group ring ZH. Deriving, first, certain classgroup invariants for locally free ZH-modules, we shall then determine those for the module in terms of the arithmetic invariants of N/Q. When 1 ≡ – 1 (mod 4), this yields again a Galois module interpretation of Artin root numbers quite analogous to that in (2). On the other hand for l ≡ 1 (mode 4), we shall get a weak ‘normal integral basis theorem’. The original impetus for this work came from computations of J. Queyrut, who – in different language – obtained these results in the case l = 3, r = 1 (cf. (7)). The tools, we are using, come from the general theory developed in recent years with such concrete applications in mind, and it is perhaps of interest to see how the various ‘strands’, on root numbers (cf. (3), (4)), on locally free modules (cf. (5)), and on Galois module structure (cf. (6)) are here pulled together. For technical reasons, we shall impose on N the slight further restriction, that l be non-ramified, although our results would remain true without this. Both the statements and the proofs of the theorem depend on ideas contained in (5) and (6). The reader who is prepared to take them for granted should, however, be able to read the present paper independently of those papers.

In the proof of the Freudenthal–Weil theorem in, for example (5), essential use is made of the fact that if G and H are compact analytic groups and ø: G → H is a continuous epimorphism then ø(Z(G)0) = Z(H)0 where the subscript 0 denotes the identity component of a topological group G and Z(G) its centre. Although this is sufficient for the proof of the Freudenthal–Weil theorem it raises the interesting question as to whether actually ø(Z(G)) = Z(H) (from which the above would follow) and, if so, in what generality this can be expected. The present paper deals with this question, in more general form, as well as certain of its structural consequences.

All sets considered in this paper will be subsets of n-dimensional Eucidean space En. In this paper, we shall consider the ‘total edge-lengths’ of polytopes which are inscribed in a given sphere and which contain its centre. We first, however, mention some related problems considered by various authors which may be of interest to the reader.

Let E be a real or complex n-dimensional normed space. Deschaseaux (1) has shown that if the absolutely summing constant π1(E) = n then E is isometrically isomorphic to . (For the definition of π1(E) and related quantities, see (2).) It is well-known ((3), (4) and (6)) that if E is a P1-space then E is isometrically isomorphic to . We shall show that Deschaseaux' result follows easily from this, and from the following elementary result: Proposition. If S is a linear operator on a real or complex n-dimensional normed space E, then |trace S| ≤ ‖S‖, with equality if and only if S is a scalar multiple of the identity I.

Let H be a complex Hilbert space. Recall that a bounded linear operator A, on H, is positive if (Ax, x) ≥ 0 (x ∈ H) (so that A = A* necessarily) and positive definite if A is positive and invertible.

Let α be an irrational p-adic number, r an arbitrary positive integer. Our aim is to prove that there exists a rational integer X satisfying

such that every possible sequence of r digits 0, 1, …, p – 1 occurs infinitely often in the canonical p-adic series for Xα. It is clear that it suffices to prove this result for p-adic integers.

Previous investigations by the author into the Stokes phenomenon pertaining to solutions of the differential equation dnu/dzn = (–1)nzmu are extended in order to find when different equations have the same set of Stokes multipliers, with perhaps a series of zeros being additionally allowed. The reason for periodic cycles to exist (with n fixed and m varying), with the same Stokes multipliers regained after a complete cycle, is traced to certain transformation properties of the equations. Within the first cycle (with n fixed and m varying) further remarkable identities exist between the Stokes multipliers, and this also is traced to special transformations between the equations. Relations are found toexist when values of m are chosen so that the highest common factors of the two integers n and n/(n + m) are identical. Finally, a transformation of the independent variable is deduced whereby the set of Stokes multipliers for an equation of order n is identical (apart from the additional zeros) to that for an equation of lower order. A hierarchy of equations is thrown up, whereby certain basic equations are transformed to yield more advanced equations of higher order and different m.

Algorithms are developed for the numerical solution of systems of first-order ordinary differential equations, the solutions of which have widely different rates of variation. The iterative procedures described use a step length of integration proportional to the rate of change of the required slowly varying solution in a region of integration, where either the transient components of the complete solution have become negligible compared with the chosen working accuracy or in a region where rapidly increasing components of the solution are theoretically possible but are made absent by the initial conditions. Several numerical examples are given to demonstrate the algorithms.

The possibility of constructing a quantum field theory by means of fields on Euclidean space is based on works by Schwinger and Symanzik (1). Probabilistic methods were used and Nelson has shown (2) that from so-called ‘Markoff fields’ one can construct Wightman fields. This idea turned out to be unusually fruitful as it made available the statistical mechanic's techniques for consideration of quantumfield theory problems. See for example (7). However as in the Minkowski space approach, the only two-dimensional space-time nontrivial models have been proved to fulfil all Wightman axioms. Since the problem for higher dimension theories is still open and extremely difficult, it is useful to have at least some criterion which allows us to eliminate certain procedures as leading to trivial theories. One such criterion existing in the Minkowski space approach is described by a notion of Borchers class (5).

This paper derives some sufficient conditions for the global validity of projective relativity theory. The basic object of study is the infinitesimal bundle, which is a generalization of a principal circle bundle. A method ofconstructing infinitesimal bundles is developed. The main result is that ifspacetime is non-compact and simply connected, and has a finite homology basis, then projective relativity is globally valid.

The de Sitter group, Spin (4, 1), is a simply connected, semi-simple, ten-dimensional Lie group which can be contracted to the inhomogeneous Lorentz group. Physical systems with the de Sitter group as asymmetry group should resemble those of the inhomogeneous Lorentz group and may provide an alternative to these systems of special-relativistic physics. Details of physics in de Sitter space from the group theoretical view-point are given in (3). The de Sitter group is also known to be a symmetry group for the bound states of the hydrogen atom, and recent work has shown how this group acts on the corresponding classical system, the Kepler problem. See (8).

This paper is concerned with a particular class of acceleration waves in heat-conducting elastic materials, namely those waves for which the acceleration amplitude is a proper vector of both the isothermal and isentropic acoustical tensors. Acceleration waves with this characteristic property are found to fall naturally into two distinct sub-classes, and close parallels are shown to exist between the members of the sub-classes and waves for which the acceleration amplitude is either longitudinal or transverse to the direction of propagation. Particular attention is given here to waves of the quasi-longitudinal type, the quasi-transverse variety having been studied in some detail elsewhere.