Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Woods, A.R.
1998.
Unsatisfiable systems of equations, over a finite field.
p.
202.
Evans, Steven
2006.
The expected number of zeros of a random system of $p$-adic polynomials.
Electronic Communications in Probability,
Vol. 11,
Issue. none,


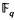 be the finite field with
be the finite field with 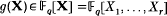 and a
and a