Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Andersson, K. G.
and
Melrose, R. B.
1977.
The propagation of singularities along gliding rays.
Inventiones Mathematicae,
Vol. 41,
Issue. 3,
p.
197.
Taylor, Michael E.
1978.
Propagation, reflection, and diffraction of singularities of solutions to wave equations.
Bulletin of the American Mathematical Society,
Vol. 84,
Issue. 4,
p.
589.
Sjöstrand, Johannes
1979.
Réflexion des singularités analytiques.
Journées équations aux dérivées partielles,
p.
1.
Sjöstrand, Johannes
1980.
Propagation of analytic singularities for second order dirichlet problems.II.
Communications in Partial Differential Equations,
Vol. 5,
Issue. 2,
p.
187.
Sjöstrand, Johannes
1980.
Complex Analysis, Microlocal Calculus and Relativistic Quantum Theory.
Vol. 126,
Issue. ,
p.
200.
Sjöstrand, Johannes
1980.
Propagation of analytic singularities for second order dirichlet problems.
Communications in Partial Differential Equations,
Vol. 5,
Issue. 1,
p.
41.
Helffer, Bernard
1980.
Séminaire Bourbaki vol. 1978/79 Exposés 525 – 542.
Vol. 770,
Issue. ,
p.
1.
Friedlander, F. G.
1981.
Singularities in Boundary Value Problems.
p.
55.
Sjöstrand, Johannes
1981.
Singularities in Boundary Value Problems.
p.
235.
Kataoka, Kiyoomi
1981.
Singularities in Boundary Value Problems.
p.
121.
Laubin, Pascal
1986.
Advances in Microlocal Analysis.
p.
165.
Mizohata, S.
Ohya, Y.
and
Ikawa, M.
1986.
Hyperbolic Equations and Related Topics.
p.
ix.
Lebeau, G.
1986.
Advances in Microlocal Analysis.
p.
203.
Laubin, Pascal
1987.
Pseudo-Differential Operators.
Vol. 1256,
Issue. ,
p.
294.
Laubin, P.
and
Willems, B.
1994.
Distributions Associated to a 2-Microlocal Pair of Lagrangian Mainfolds.
Communications in Partial Differential Equations,
Vol. 19,
Issue. 9-10,
p.
101.
Lafitte, Olivier
1995.
The kernel of the neumann operator for a strictly diffractive analytic problem.
Communications in Partial Differential Equations,
Vol. 20,
Issue. 3-4,
p.
419.
Laubin, P.
1997.
Microlocal Analysis and Spectral Theory.
p.
91.
Lafitte, Olivier D.
1998.
Diffraction in the High Frequency Regime by a Thin Layer of Dielectric Material II: the Trace of the Wave in the Shadow of the Obstacle.
SIAM Journal on Applied Mathematics,
Vol. 59,
Issue. 3,
p.
1053.
Laubin, Pascal
1999.
On the Lagrangian regularity near non-transversal crossing of Lagrangian manifolds.
ANNALI DELL UNIVERSITA DI FERRARA,
Vol. 45,
Issue. 1,
p.
197.
Laubin, Pascal
2003.
Jean Leray ’99 Conference Proceedings.
p.
83.
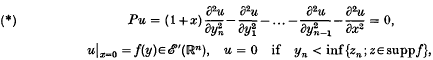
 +, y∈
+, y∈ n, and n > 1; the precise meaning of the boundary condition at x = 0 is explained in section 1 below. The principal result of [I] can be expressed concisely by saying that singularities do not propagate along the boundary; a detailed statement is given in Theorem 1·9 of the present paper.
n, and n > 1; the precise meaning of the boundary condition at x = 0 is explained in section 1 below. The principal result of [I] can be expressed concisely by saying that singularities do not propagate along the boundary; a detailed statement is given in Theorem 1·9 of the present paper.