Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-09T08:46:28.181Z Has data issue: false hasContentIssue false
  • English
  • Français

Wald's identity and absorption probabilities for two-dimensional random walks

Published online by Cambridge University Press:  24 October 2008

V. D. Barnett
V. D. Barnett
Affiliation:
University of Birmingham
Get access Rights & Permissions [Opens in a new window]

Summary

Suppose a particle executes a random walk on a two-dimensional square lattice, starting at the origin. The position of the particle after n steps of the walk is Xn = (Xl, n, X2n), where

and we will assume that the Yi are independent bivariate discrete random variables with common moment generating function (m.g.f.)

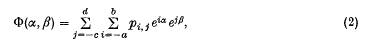
where a, b, c and d are non-negative. We assume further that (i) pi, j is non-zero for some finite positive and negative i, and some finite positive and negative j (− a ≤ i ≤ b, − c ≤ jd), such values of i and j including – a, b and – c, d, respectively, whenever a, b, c or d is finite, and (ii) the double series defining Φ(α, β) is convergent at least in some finite region D, of the real (α, β) plane, which includes the origin.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 61 , Issue 3 , July 1965 , pp. 747 - 762
Copyright
Copyright © Cambridge Philosophical Society 1965

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

(1)Barnett, V. D.Some explicit results for an asymmetric two-dimensional random walk. Proc. Cambridge Philos. Soc. 59 (1963), 451–62.CrossRefGoogle Scholar
(2)Chung, K. L and Fuchs, W. H. T.On the distribution of values of sums of random variables. Mem. Amer. Math. Soc. 6 (1951), 2–14.Google Scholar
(3)Henze, E.Zur Theorie der diskreten unsymmetrischen Irrfahrt. Z. Angew. Math. Mech. 41 (1961), 1–9.CrossRefGoogle Scholar
(4)Kemperman, J. H. B.The passage problem for a stationary Markov chain (Chicago, 1961).CrossRefGoogle Scholar
(5)Kingman, J. F. C.The ergodic behaviour of random walks. Biometrika 48 (1961), 391–6.CrossRefGoogle Scholar
(6)Lindley, D. V.The theory of queues with a single server. Proc. Cambridge Philos. Soc. 48 (1952), 277–89.CrossRefGoogle Scholar
(7)Miller, H. D.A generalisation of Wald's identity with applications to random walks. Ann. Math. Statist. 32 (1961), 549–60.CrossRefGoogle Scholar
(8)Wald, A.Sequential analysis (Wiley; London, 1947).Google Scholar