Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T21:10:21.875Z Has data issue: false hasContentIssue false
  • English
  • Français

A variant of the Corners theorem

Part of: Sequences and sets Extremal combinatorics

Published online by Cambridge University Press:  02 February 2021

MATEI MANDACHE
MATEI MANDACHE*
Affiliation:
Mathematical Institute, University of Oxford, Oxford. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The Corners theorem states that for any α > 0 there exists an N0 such that for any abelian group G with |G| = N ≥ N0 and any subset A ⊂ G×G with |A| ≥ αN2 we can find a corner in A, i.e. there exist x, y, d ∈ G with d ≠ 0 such that (x,y),(x+d,y),(x,y+d) ∈ A.

Here, we consider a stronger version, in which we try to find many corners of the same size. Given such a group G and subset A, for each d ∈ G we define Sd={(x,y) ∈ G × G: (x,y),(x+d,y),(x,y+d) ∈ A}. So |Sd| is the number of corners of size d. Is it true that, provided N is sufficiently large, there must exist some d ∈G\{0} such that |Sd|>(α3-ϵ)N2?

We answer this question in the negative. We do this by relating the problem to a much simpler-looking problem about random variables. Then, using this link, we show that there are sets A with |Sd|>Cα3.13N2 for all d ≠ 0, where C is an absolute constant. We also show that in the special case where 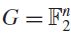$G = {\mathbb{F}}_2^n$, one can always find a d with |Sd|>(α4-ϵ)N2.

MSC classification

Primary: 11B30: Arithmetic combinatorics; higher degree uniformity
Secondary: 05D05: Extremal set theory
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 171 , Issue 3 , November 2021 , pp. 607 - 621
Copyright
© Cambridge Philosophical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ajtai, M. and Szemerédi, E.. Sets of lattice points that form no squares. Stud. Sci. Math. Hungar. 9 (1975), 9–11.Google Scholar
Bergelson, V., Host, B., and Kra, B.. Multiple recurrence and nilsequences. Invent. Math. 160(2) (2005), 261–303. With an appendix by Imre Ruzsa.CrossRefGoogle Scholar
Qing, Chu. Multiple recurrence for two commuting transformations. Ergodic Theory Dynam. Systems 31(3) (2011), 771–792.Google Scholar
Fox, J., Sah, A., Sawhney, M., Stoner, D. and Zhao, Y.. Triforce and corners. Math. Proc. Camb. Phil. Soc. (2019), 1–15.CrossRefGoogle Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory (Princeton University Press, Princeton, N.J., 1981). M. B. Porter Lectures.CrossRefGoogle Scholar
Green, B.. A Szemerédi-type regularity lemma in abelian groups, with applications. Geom. Funct. Anal. 15(2) (2005), 340–376.CrossRefGoogle Scholar
Green, B. and Tao, T.. An arithmetic regularity lemma, an associated counting lemma, and applications. In An irregular mind, volume 21 of Bolyai Soc. Math. Stud. (János Bolyai Math. Soc., Budapest, 2010), pages 261–334.CrossRefGoogle Scholar
Hoeffding, W.. Probability inequalities for sums of bounded random variables. J. Amer. Statist. Assoc., 58 (1963), 13–30.CrossRefGoogle Scholar
Mandache, M.. A variant of the corner theorem. Preprint, arXiv:1804.03972 (2018).Google Scholar
Ruzsa, I. Z. and Szemerédi, E.. Triple systems with no six points carrying three triangles. In Combinatorics (Proc. Fifth Hungarian Colloq., Keszthely, 1976), Vol. II, volume 18 of Colloq. Math. Soc. János Bolyai. (North-Holland, Amsterdam-New York, 1978), pages 939–945.Google Scholar
Shkredov, I. D.. On a problem of Gowers. Izv. Ross. Akad. Nauk Ser. Mat. 70(2) (2006), 179–221.Google Scholar
Szemerédi, E.. On sets of integers containing no k elements in arithmetic progression. Acta Arith. 27 (1975), 199–245. Collection of articles in memory of Juri Vladimirovič Linnik.CrossRefGoogle Scholar
Szemerédi, E.. Regular partitions of graphs. In Problèmes combinatoires et théorie des graphes (Colloq. Internat. CNRS, Univ. Orsay, Orsay, 1976), volume 260 of Colloq. Internat. CNRS, (CNRS Paris, 1978), pages 399–401.Google Scholar