Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T13:31:55.602Z Has data issue: false hasContentIssue false
  • English
  • Français

A variant of the Bombieri–Vinogradov theorem in short intervals and some questions of Serre

Published online by Cambridge University Press:  22 February 2016

JESSE THORNER
JESSE THORNER*
Affiliation:
Department of Mathematics and Computer Science, Emory University, Atlanta, Georgia, U.S.A. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We generalise the classical Bombieri–Vinogradov theorem for short intervals to a non-abelian setting. This leads to variants of the prime number theorem for short intervals where the primes lie in arithmetic progressions that are “twisted” by a splitting condition in a Galois extension of number fields. Using this result in conjunction with the recent work of Maynard, we prove that rational primes with a given splitting condition in a Galois extension L/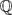$\mathbb{Q}$ exhibit bounded gaps in short intervals. We explore several arithmetic applications related to questions of Serre regarding the non-vanishing Fourier coefficients of cuspidal modular forms. One such application is that for a given modular L-function L(s, f), the fundamental discriminants d for which the d-quadratic twist of L(s, f) has a non-vanishing central critical value exhibit bounded gaps in short intervals.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 161 , Issue 1 , July 2016 , pp. 53 - 63
Copyright
Copyright © Cambridge Philosophical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Balog, A. and Ono, K.The Chebotarev density theorem in short intervals and some questions of Serre. J. Number Theory. 91 (2001), no. 2, 356–371.CrossRefGoogle Scholar
[2]Bartz, K. M.An effective order of Hecke-Landau zeta functions near the line σ = 1. II. (Some applications). Acta Arith. 52 (1989), no. 2, 163–170.Google Scholar
[3]Freiberg, T.A Note on the Theorem of Maynard and Tao. Advances in the Theory of Numbers. Proc. Thirteenth Conference of the Canadian Number Theory Association. (2015), pp. 87–103.Google Scholar
[4]Goldfeld, D.Conjectures on Elliptic Curves Over Quadratic Fields. Number Theory, Carbondale 1979 (Proc. Southern Illinois Conf., Southern Illinois Univ., Carbondale, Ill., 1979). (1979), pp. 108–118. Berlin.CrossRefGoogle Scholar
[5]Heath-Brown, D. R.On the density of the zeros of the Dedekind zeta-function. Acta Arith. 33 (1977), no. 2, 169–181.Google Scholar
[6]Hinz, J.Über Nullstellen der Heckeschen Zetafunctionen in algebraischen Zahlkörpern. Acta Arith. 31 (1976), no. 2, 167–193.Google Scholar
[7]Huxley, M. N. and Iwaniec, H.Bombieri's theorem in short intervals. Mathematika 22 (1975), no. 2, 188–194.Google Scholar
[8]Kolyvagin, V. A.Finiteness of E(Q) and SH(E,Q) for a subclass of Weil curves. Izv. Akad. Nauk SSSR Ser. Mat. 52 (1988), no. 3, 522–540, 670–671.Google Scholar
[9]Lagarias, J. C. and Odlyzko, A. M.Effective Versions of the Chebotarev Density Theorem. Algebraic Number Fields: L-functions and Galois properties (Proc. Sympos., University Durham, Durham, 1975). (1977), pp. 409–464.Google Scholar
[10]Maynard, J. Dense clusters of primes in subsets. arxiv.org/abs/1405.2593.Google Scholar
[11]Maynard, J.Small gaps between primes. Ann. of Math. (2) 181 (2015), no. 1, 383–413.Google Scholar
[12]Montgomery, H. L.Topics in multiplicative number theory. Lecture Notes in Math., Vol. 227. (Springer-Verlag, Berlin-New York, 1971).CrossRefGoogle Scholar
[13]Murty, M. R. and Murty, V. K. A variant of the Bombieri–Vinogradov theorem. Number Theory (Montreal, Que., 1985). (1987), pp. 243–272.Google Scholar
[14]Murty, M. R., Murty, V. K. and Saradha, N.Modular forms and the Chebotarev density theorem. Amer. J. Math. 110(1988), no. 2, 253–281.Google Scholar
[15]Murty, M. R. and Petersen, K. L.A Bombieri–Vinogradov theorem for all number fields. Trans. Amer. Math. Soc. 365 (2013), no. 9, 4987–5032.Google Scholar
[16]Murty, V. K. Modular forms and the Chebotarev density theorem. II. Analytic Number Theory (Kyoto, 1996). (1997), pp. 287–308.Google Scholar
[17]Ono, K.Nonvanishing of quadratic twists of modular L-functions and applications to elliptic curves. J. Reine Angew. Math. 533 (2001), 81–97.Google Scholar
[18]Ono, K.The Web of Modularity: Arithmetic of the Coefficients of Modular Forms and q-Series. CBMS Regional Conference Series in Mathematics. vol. 102. Published for the Conference Board of the Mathematical Sciences, Washington, DC (American Mathematical Society, Providence, RI, 2004).Google Scholar
[19]Ono, K. and Skinner, C.Non-vanishing of quadratic twists of modular L-functions. Invent. Math. 134 (1998), no. 3, 651–660.Google Scholar
[20]Perelli, A., Pintz, J. and Salerno, S.Bombieri's theorem in short intervals. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 11 (1984), no. 4, 529–539.Google Scholar
[21]Serre, J.-P.Quelques applications du théorème de densité de Chebotarev. Inst. Hautes Études Sci. Publ. Math., (54) (1981), 323–401.Google Scholar
[22]Shimura, G.On modular forms of half integral weight. Ann. of Math. (2) 97 (1973), 440–481.Google Scholar
[23]Shiu, D. K. L.Strings of congruent primes. J. London Math. Soc. (2) 61 (2000), no. 2, 359–373.Google Scholar
[24]Thorner, J.Bounded gaps between primes in Chebotarev sets. Res. Math. Sci. 1 (2014), Art. 4, 16.Google Scholar
[25]Timofeev, N. M.Distribution of arithmetic functions in short intervals in the mean with respect to progressions. Izv. Akad. Nauk SSSR Ser. Mat. 51 (1987), no. 2, 341–362, 447.Google Scholar
[26]Waldspurger, J.-L.Sur les coefficients de Fourier des formes modulaires de poids demi-entier. J. Math. Pures Appl. (9) 60 (1981), no. 4, 375–484.Google Scholar
[27]Wan, D. Q.On the Lang–Trotter conjecture. J. Number Theory. 35 (1990), no. 3, 247–268.Google Scholar