Published online by Cambridge University Press: 24 October 2008
Assuming that the solute and solvent molecules in a solution can be regarded as occupying sites on a regular lattice and that the potential energy arises from interactions between molecules which occupy closest neighbour sites, the vapour-pressure equations have been determined for solutions in which each solute molecule contains three groups (or submolecules) and occupies three lattice sites in such a way that successive submolecules occupy closest neighbour sites on the lattice while each solvent molecule occupies only one site. The vapour-pressure equations are compared with those which have already been obtained by Fowler and Guggenheim for the case in which each solute molecule contains two submolecules in order to determine the effect on the form of the vapour-pressure equations of the number of submolecules in each solute molecule. This enables the determination of the vapour-pressure equations when each solute molecule contains n submolecules and occupies n lattice sites in such a way that successive submolecules occupy closest neighbour sites on the lattice. In this latter case the vapour-pressure equations are
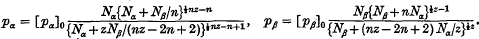
These equations are used to determine the osmotic pressure of solutions of long-chain polymers, and it is found that in the region of osmotic interest, the osmotic pressure is given by an equation of the form
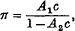
where c g. of solute per 100 c.c. of solution is the concentration. It is shown that this equation can be written approximately
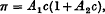
which is the quadratic relation which has usually been fitted to osmotic measurements. To this approximation π/c plotted as a function of c gives a straight line of which the intercept on the π/c axis determines the molecular weight of the polymer molecule and the gradient determines the number of submolecules in each polymer molecule.