Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-10T21:13:26.966Z Has data issue: false hasContentIssue false
  • English
  • Français

Units of group rings, the Bogomolov multiplier and the fake degree conjecture

Published online by Cambridge University Press:  09 September 2016

JAVIER GARCÍA–RODRÍGUEZ ,
ANDREI JAIKIN–ZAPIRAIN  and
URBAN JEZERNIK
JAVIER GARCÍA–RODRÍGUEZ
Affiliation:
Departamento de Matemáticas, Universidad Autónoma de Madrid and Instituto de Ciencias Matemáticas (ICMAT), Madrid, Spain. e-mails: [email protected]; [email protected]
ANDREI JAIKIN–ZAPIRAIN
Affiliation:
Departamento de Matemáticas, Universidad Autónoma de Madrid and Instituto de Ciencias Matemáticas (ICMAT), Madrid, Spain. e-mails: [email protected]; [email protected]
URBAN JEZERNIK
Affiliation:
Faculty of Mathematics and Physics, University of Ljubljana, Ljubljana, Slovenia. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let π be a finite p-group and 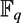${\mathbb{F}_{q}}$ a finite field with q = pn elements. Denote by 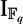$\I_{\mathbb{F}_{q}}$ the augmentation ideal of the group ring 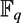${\mathbb{F}_{q}}$[π]. We have found a surprising relation between the abelianization of 1 + 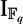$\I_{\mathbb{F}_{q}}$, the Bogomolov multiplier B0(π) of π and the number of conjugacy classes k(π) of π:

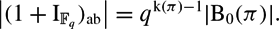$$ \left | (1+\I_{\Fq})_{\ab} \right |=q^{\kk(\pi)-1}|\!\B_0(\pi)|.
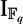In particular, if π is a finite p-group with a non-trivial Bogomolov multiplier, then 1 + $\I_{\mathbb{F}_{q}}$ is a counterexample to the fake degree conjecture proposed by M. Isaacs.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 163 , Issue 1 , July 2017 , pp. 115 - 123
Copyright
Copyright © Cambridge Philosophical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Bass, H. Algebraic K-Theory (W. A. Benjamin, 1968).Google Scholar
[2] Bogomolov, F. A. The Brauer group of quotient spaces by linear group actions. Izv. Akad. Nauk SSSR Ser. Mat. 51 (1987), 485–516 (English transl. Math. USSR Izv. 30 (1988), 455–485).Google Scholar
[3] Borel, A. Linear algebraic groups. Graduate Texts in Mathematics 126 (Springer-Verlag, 1991).Google Scholar
[4] Chu, H., Hu, S., Kang, M. and Kunyavskiĭ, B. E. Noether's problem and the unramified Brauer group for groups of order 64. Int. Math. Res. Not. 12 (2010), 2329–2366.Google Scholar
[5] Bovdi, V., Konovalov, A., Rossmanith, R. and Schneider, C. LAGUNA – Lie AlGebras and UNits of group Algebras. Version 3.6.2. 2013 (http://www.cs.st-andrews.ac.uk/alexk/laguna/).Google Scholar
[6] Hoshi, A., Kang, M. and Kunyavskiĭ, B. E. Noether's problem and unramified Brauer groups. Asian J. Math. 17 (2013), 689–714.CrossRefGoogle Scholar
[7] Humphreys, J. E. Linear algebraic groups. Graduate Texts in Mathematics 21 (Springer-Verlag, 1975).Google Scholar
[8] Jaikin-Zapirain, A. A counterexample to the fake degree conjecture. Chebyshevskii Sb. 5 (2004), 188–192.Google Scholar
[9] Jaikin-Zapirain, A. Zeta function of representations of compact p-adic analytic groups. J. Amer. Math. Soc. 19 (2006), 91–118.Google Scholar
[10] Jezernik, U. and Moravec, P. Bogomolov multipliers of groups of order 128. Exp. Math. 23 (2014), 174–180.Google Scholar
[11] Kambayashi, T., Miyanishi, M. and Takeuchi, M. Unipotent algebraic groups. Lecture Notes in Mathematics 144 (Springer-Verlag, 1974).CrossRefGoogle Scholar
[12] Kang, M. C. Bogomolov multipliers and retract rationality for semidirect products. J. Algebra 397 (2014), 407–425.Google Scholar
[13] Kazhdan, D. Proof of Springer's Hypothesis. Israel J. Math. 28 (1977), 272–286.Google Scholar
[14] Moravec, P. Schur multipliers and power endomorphisms of groups. J. Algebra 308 (2007), 12–25.Google Scholar
[15] Moravec, P. Unramified groups of finite and infinite groups. Amer. J. Math. 134 (2012), 1679–1704.CrossRefGoogle Scholar
[16] Neumann, W. D. Manifold cutting and pasting groups. Topology 14 (1975), 237–244.Google Scholar
[17] Oliver, R. SK1 for finite group rings: II. Math. Scand. 47 (1980), 195–231.Google Scholar
[18] Rosenberg, J. Algebraic K-theory and its applications. Graduate Texts in Mathematics 147 (Springer-Verlag, 1994).CrossRefGoogle Scholar
[19] Sangroniz, J. Characters of algebra groups and unitriangular groups. Finite Groups 2003 (Walter de Gruyter, 2004).Google Scholar
[20] Schur, I. Über die Darstellung der endlichen Gruppen durch gebrochene lineare Substitutionen. J. Reine Angew. Math. 127 (1904), 20–50.Google Scholar
[21] Wall, C. T. C. Norms of units in group rings. Proc. London Math. Soc. (3) 29 (1974), 593–632.Google Scholar