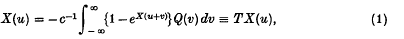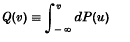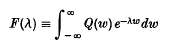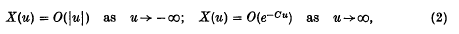Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
1977.
Discussion of Dr Mollison's Paper.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 39,
Issue. 3,
p.
314.
Diekmann, Odo
and
Kaper, Hans G.
1978.
On the bounded solutions of a nonlinear convolution equation.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 2,
Issue. 6,
p.
721.
Lui, Roger
1982.
A Nonlinear Integral Operator Arising from a Model in Population Genetics I. Monotone Initial Data.
SIAM Journal on Mathematical Analysis,
Vol. 13,
Issue. 6,
p.
913.
Radcliffe, J.
Rass, L.
and
Stirling, W. D.
1982.
Wave solutions for the deterministic host-vector epidemic.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 91,
Issue. 1,
p.
131.
Ball, Frank G.
1991.
Dynamic population epidemic models.
Mathematical Biosciences,
Vol. 107,
Issue. 2,
p.
299.
Ruan, Shigui
2006.
Mathematics for Life Science and Medicine.
p.
97.
Thieme, Horst
2006.
Mathematical Biosciences,
Vol. 202,
Issue. 1,
p.
218.
Ai, Shangbing
and
Albashaireh, Reem
2014.
Traveling Waves in Spatial SIRS Models.
Journal of Dynamics and Differential Equations,
Vol. 26,
Issue. 1,
p.
143.
Zhao, Lin
and
Wang, Zhi-Cheng
2016.
Traveling wave fronts in a diffusive epidemic model with multiple parallel infectious stages.
IMA Journal of Applied Mathematics,
Vol. 81,
Issue. 5,
p.
795.
Zhao, Lin
Wang, Zhi-Cheng
and
Ruan, Shigui
2017.
Traveling wave solutions in a two-group epidemic model with latent period.
Nonlinearity,
Vol. 30,
Issue. 4,
p.
1287.
Khachatryan, A. Kh.
Khachatryan, Kh. A.
and
Petrosyan, H. S.
2021.
Solvability of Two-Dimensional Integral Equations with Monotone Nonlinearity.
Journal of Mathematical Sciences,
Vol. 257,
Issue. 5,
p.
720.
Khachatryan, A. Kh.
Khachatryan, Kh. A.
and
Petrosyan, H. S.
2021.
On Positive Bounded Solutions of One Class
of Nonlinear Integral Equations
with the Hammerstein–Nemytskii Operator.
Differential Equations,
Vol. 57,
Issue. 6,
p.
768.
Khachatryan, Kh. A.
and
Petrosyan, H. S.
2022.
Asymptotic Behavior of the Solution for One Class of Nonlinear Integral Equations of Hammerstein Type on the Whole Axis.
Contemporary Mathematics. Fundamental Directions,
Vol. 68,
Issue. 2,
p.
376.
Khachatryan, Kh. A.
and
Petrosyan, H. S.
2024.
Asymptotic Behavior of the Solution for One Class of Nonlinear Integral Equations of Hammerstein Type on the Whole Axis.
Journal of Mathematical Sciences,
Vol. 282,
Issue. 2,
p.
292.
Zhao, Lin
and
Liu, Yini
2025.
Time periodic traveling wave solutions of a time-periodic reaction–diffusion SEIR epidemic model with periodic recruitment.
Nonlinear Analysis: Real World Applications,
Vol. 81,
Issue. ,
p.
104167.