Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T07:40:58.438Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniformly asymptotic expansions for an integral with a large and a small parameter

Published online by Cambridge University Press:  24 October 2008

F. Ursell
F. Ursell
Affiliation:
Department of Mathematics, University of Manchester, Manchester M13 9PL
Get access Rights & Permissions [Opens in a new window]

Abstract

The integral

involves a large real parameter N and a small real parameter ∈. Its asymptotic behaviour is non-uniform when N → ∞ and ∈ → 0. Thus, when ∈ > 0 is kept fixed and N → ∞, the integral decays exponentially at a rate depending on ∈; when ∈ → 0 the integral tends to

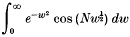
which decays algebraically when N → ∞. It is shown that several distinct uniformly asymptotic expansions can be obtained which each involve an infinite set of functions of the combination 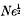Certain related integrals are also treated.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 101 , Issue 2 , March 1987 , pp. 349 - 362
Copyright
Copyright © Cambridge Philosophical Society 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Chester, C., Friedman, B. and Ursell, F.. An extension of the method of steepest descents. Proc. Cambridge Philos. Soc. 53 (1957), 599–611.CrossRefGoogle Scholar
[2]Olver, F. W. J.. Asymptotics and special functions (Academic Press, 1974).Google Scholar
[3]Robbins, C. I. and Smith, R. C. T.. A table of roots of sin Z = − Z. Phil. Mag. (7) 39 (1948), 1004–1005.CrossRefGoogle Scholar
[4]Ursell, F.. Integrals with a large parameter. The continuation of uniformly asymptotic expansions. Proc. Cambridge Philos. Soc. 61 (1965), 113–128.CrossRefGoogle Scholar
[5]Ursell, F.. Integrals with a large parameter. Several nearly coincident saddle points. Proc. Cambridge Philos. Soc. 72 (1972), 49–65.CrossRefGoogle Scholar