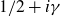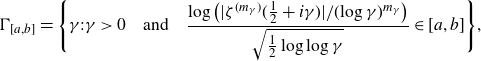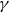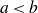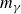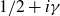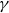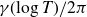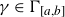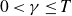1. Introduction
It is well known that the positive ordinates
![]() ${\gamma }$
of the nontrivial zeros
${\gamma }$
of the nontrivial zeros
![]() ${\rho }={\beta}+i{\gamma }$
of the Riemann zeta function, when arranged in increasing order, are uniformly distributed modulo one. This was proved by Rademacher [
Reference Rademacher7
] in the 1950s under the assumption of the Riemann hypothesis. Elliott [
Reference Elliott3
] later pointed out that this could be shown unconditionally. Our aim in this paper is to prove that if the Riemann hypothesis holds and a plausible hypothesis about the spacing of the
${\rho }={\beta}+i{\gamma }$
of the Riemann zeta function, when arranged in increasing order, are uniformly distributed modulo one. This was proved by Rademacher [
Reference Rademacher7
] in the 1950s under the assumption of the Riemann hypothesis. Elliott [
Reference Elliott3
] later pointed out that this could be shown unconditionally. Our aim in this paper is to prove that if the Riemann hypothesis holds and a plausible hypothesis about the spacing of the
![]() ${\gamma }$
’s is true, then the
${\gamma }$
’s is true, then the
![]() ${\gamma }$
are also uniformly distributed modulo one when we restrict to certain subsequences.
${\gamma }$
are also uniformly distributed modulo one when we restrict to certain subsequences.
Throughout we assume the Riemann hypothesis so that every nontrivial zero of the zeta function has the form
![]() ${\rho }=1/2+i{\gamma }$
. Then N(T), the number of ordinates
${\rho }=1/2+i{\gamma }$
. Then N(T), the number of ordinates
![]() ${\gamma }$
in the interval (0, T] is given by
${\gamma }$
in the interval (0, T] is given by
(see Titchmarsh [
Reference Titchmarsh8
, chapter 14]). Note that unconditionally, the error term is
![]() $O(\!\log T)$
. We also assume that for some
$O(\!\log T)$
. We also assume that for some
![]() $0<{\delta} \leq 1$
the following spacing hypothesis holds for the zeros.
$0<{\delta} \leq 1$
the following spacing hypothesis holds for the zeros.
Hypothesis
![]() $\mathcal{H}_\delta$
1. Let
$\mathcal{H}_\delta$
1. Let
![]() ${\gamma }^+$
be the next larger ordinate of a zero of the zeta function after the ordinate
${\gamma }^+$
be the next larger ordinate of a zero of the zeta function after the ordinate
![]() ${\gamma }$
with the understanding that
${\gamma }$
with the understanding that
![]() ${\gamma }^+={\gamma }$
if and only if
${\gamma }^+={\gamma }$
if and only if
![]() $1/2+i{\gamma }$
is a multiple zero. Then there exists a positive constant M such that, uniformly for
$1/2+i{\gamma }$
is a multiple zero. Then there exists a positive constant M such that, uniformly for
![]() $0<{\lambda}<1$
, we have
$0<{\lambda}<1$
, we have
Hypothesis
![]() $\mathscr{H}_{\delta}$
is credible because Hypothesis
$\mathscr{H}_{\delta}$
is credible because Hypothesis
![]() $\mathscr{H}_{1}$
follows from Montgomery’s pair correlation conjecture which, in turn, implies Hypothesis
$\mathscr{H}_{1}$
follows from Montgomery’s pair correlation conjecture which, in turn, implies Hypothesis
![]() $\mathscr{H}_{\delta}$
for every
$\mathscr{H}_{\delta}$
for every
![]() $\delta \in (0, 1]$
. Notice also that Hypothesis
$\delta \in (0, 1]$
. Notice also that Hypothesis
![]() $\mathscr{H}_{\delta}$
implies that all but o(N(T)) of the zeros are simple, a fact we shall use later.
$\mathscr{H}_{\delta}$
implies that all but o(N(T)) of the zeros are simple, a fact we shall use later.
Let
![]() $m_{\gamma }$
denote the multiplicity of the zero
$m_{\gamma }$
denote the multiplicity of the zero
![]() ${\rho }=\frac12+i{\gamma }$
, and let
${\rho }=\frac12+i{\gamma }$
, and let
![]() $a<b$
be real numbers. The sequences we wish to consider are
$a<b$
be real numbers. The sequences we wish to consider are
 \begin{equation*} {\Gamma }_{[a, b] }= \Bigg\{ {\gamma }>0 \, : \, \frac{ \log(\big| \zeta^{(m_{\gamma })} (\frac12+ i{\gamma }) \big| / (\!\log{{\gamma }} )^{m_{\gamma }} )}{\sqrt{\frac12\log\log {\gamma }}} \in [a, b] \Bigg\}\end{equation*}
\begin{equation*} {\Gamma }_{[a, b] }= \Bigg\{ {\gamma }>0 \, : \, \frac{ \log(\big| \zeta^{(m_{\gamma })} (\frac12+ i{\gamma }) \big| / (\!\log{{\gamma }} )^{m_{\gamma }} )}{\sqrt{\frac12\log\log {\gamma }}} \in [a, b] \Bigg\}\end{equation*}
and
 \begin{equation*}{ {\Gamma }}^{*}_{[a, b] }= \Bigg\{ {\gamma }>0 \, : \, m_{\gamma }=1 \; \hbox{and}\; \; \frac{ \log(\big| \zeta^{\prime} (\frac12+ i{\gamma }) \big| / \log{{\gamma }} )}{\sqrt{\frac12\log\log {\gamma }}} \in [a, b] \Bigg\},\end{equation*}
\begin{equation*}{ {\Gamma }}^{*}_{[a, b] }= \Bigg\{ {\gamma }>0 \, : \, m_{\gamma }=1 \; \hbox{and}\; \; \frac{ \log(\big| \zeta^{\prime} (\frac12+ i{\gamma }) \big| / \log{{\gamma }} )}{\sqrt{\frac12\log\log {\gamma }}} \in [a, b] \Bigg\},\end{equation*}
where the
![]() ${\gamma }$
are listed in increasing order. Our first theorem, a slight modification of a recent result of Çiçek [
Reference Çiçek2
], provides the counting functions of these sequences.
${\gamma }$
are listed in increasing order. Our first theorem, a slight modification of a recent result of Çiçek [
Reference Çiçek2
], provides the counting functions of these sequences.
Theorem 1·1. Assume the Riemann hypothesis is true and that Hypothesis
![]() $\mathscr{H}_{\delta}$
holds for some
$\mathscr{H}_{\delta}$
holds for some
![]() ${\delta}\in(0, 1]$
. Let
${\delta}\in(0, 1]$
. Let
![]() $\max(|a|, |b|)\ll (\!\log \log \log T)^{\frac12-{\epsilon}}$
, where
$\max(|a|, |b|)\ll (\!\log \log \log T)^{\frac12-{\epsilon}}$
, where
![]() ${\epsilon}>0$
. Then for all sufficiently large T,
${\epsilon}>0$
. Then for all sufficiently large T,
 \begin{equation}\begin{split}N_{[a, b]}(T)\, :\!=\, \sum_{\substack{ 0<{\gamma }\leq T \\ {\gamma }\in {\Gamma }_{[a, b] }} } 1 =\frac{N(T)}{\sqrt{2\pi} } \int_a^b e^{-{x^2}/{2}}\, dx +O\bigg( N(T)\frac{(\!\log\log\log T)^2}{\sqrt{\log\log T}} \bigg) .\end{split}\end{equation}
\begin{equation}\begin{split}N_{[a, b]}(T)\, :\!=\, \sum_{\substack{ 0<{\gamma }\leq T \\ {\gamma }\in {\Gamma }_{[a, b] }} } 1 =\frac{N(T)}{\sqrt{2\pi} } \int_a^b e^{-{x^2}/{2}}\, dx +O\bigg( N(T)\frac{(\!\log\log\log T)^2}{\sqrt{\log\log T}} \bigg) .\end{split}\end{equation}
For the sequence
![]() ${\Gamma }_{[a, b]}^*$
we have
${\Gamma }_{[a, b]}^*$
we have
 \begin{equation}\begin{split}N_{[a, b]}^*(T)\, :\!=\, \sum_{\substack{ 0<{\gamma }\leq T \\ {\gamma }\in {\Gamma }_{[a, b]}^* } } 1 = \frac{N(T) }{\sqrt{2\pi} } \int_a^b e^{-{x^2}/{2}} dx +o(N(T)).\end{split}\end{equation}
\begin{equation}\begin{split}N_{[a, b]}^*(T)\, :\!=\, \sum_{\substack{ 0<{\gamma }\leq T \\ {\gamma }\in {\Gamma }_{[a, b]}^* } } 1 = \frac{N(T) }{\sqrt{2\pi} } \int_a^b e^{-{x^2}/{2}} dx +o(N(T)).\end{split}\end{equation}
Observe that (1·3) follows immediately from (1·2) since Hypothesis
![]() $\mathscr{H}_{\delta}$
implies that all but o(N(T)) of the zeros are simple.
$\mathscr{H}_{\delta}$
implies that all but o(N(T)) of the zeros are simple.
Our next theorem is our main uniform distribution result.
Theorem 1·2. Assume the Riemann hypothesis and that Hypothesis
![]() $\mathscr{H}_{\delta}$
is true for some
$\mathscr{H}_{\delta}$
is true for some
![]() $0<{\delta}\leq 1$
. Let a and b be either fixed, or functions of T for which
$0<{\delta}\leq 1$
. Let a and b be either fixed, or functions of T for which
![]() $\max(|a|, |b|)\ll (\!\log \log \log T)^{\frac12-{\epsilon}}$
, where
$\max(|a|, |b|)\ll (\!\log \log \log T)^{\frac12-{\epsilon}}$
, where
![]() ${\epsilon}>0$
, and
${\epsilon}>0$
, and
![]() $\int_a^b e^{-x^2/2} dx \gg 1$
. Then the sequences
$\int_a^b e^{-x^2/2} dx \gg 1$
. Then the sequences
![]() ${\Gamma }_{[a, b] }$
and
${\Gamma }_{[a, b] }$
and
![]() ${\Gamma }^*_{[a, b] }$
are uniformly distributed modulo one.
${\Gamma }^*_{[a, b] }$
are uniformly distributed modulo one.
The average gap between the ordinates
![]() $ {\gamma } \in (0, T]$
is
$ {\gamma } \in (0, T]$
is
![]() $2\pi/ \log T$
by (1·1). Thus the numbers
$2\pi/ \log T$
by (1·1). Thus the numbers
![]() ${\gamma }(\!\log T)/2\pi$
have average spacing one. Not surprisingly, it is more difficult to prove that these numbers are equidistributed modulo one. In fact, it is not known. This is also true for the numbers
${\gamma }(\!\log T)/2\pi$
have average spacing one. Not surprisingly, it is more difficult to prove that these numbers are equidistributed modulo one. In fact, it is not known. This is also true for the numbers
![]() ${\gamma }(\!\log T)/2\pi$
with
${\gamma }(\!\log T)/2\pi$
with
![]() $ {\gamma } \in (0, T]$
and
$ {\gamma } \in (0, T]$
and
![]() ${\gamma }\in{\Gamma }_{[a,b]}$
or
${\gamma }\in{\Gamma }_{[a,b]}$
or
![]() ${\Gamma }_{[a,b]}^*$
. However, if we assume the following further conjecture of the second author (confer [
Reference Gonek5
]), we can show uniform distribution in all three cases.
${\Gamma }_{[a,b]}^*$
. However, if we assume the following further conjecture of the second author (confer [
Reference Gonek5
]), we can show uniform distribution in all three cases.
Conjecture 1. For
![]() $x, T \geq 2$
and any fixed
$x, T \geq 2$
and any fixed
![]() $\epsilon >0$
,
$\epsilon >0$
,
Theorem 4 of [
Reference Gonek5
] provides evidence for Conjecture 1. It says that if
![]() $\psi(y)=\sum_{n\leq y} \Lambda(n)$
, where
$\psi(y)=\sum_{n\leq y} \Lambda(n)$
, where
![]() $\Lambda(n)$
is the von Mangoldt function, then Conjecture 1 implies that
$\Lambda(n)$
is the von Mangoldt function, then Conjecture 1 implies that
for
![]() $1\leq h\leq y$
and
$1\leq h\leq y$
and
![]() $\epsilon>0$
. Conversely, (1·4) implies a weighted form of Conjecture 1, namely,
$\epsilon>0$
. Conversely, (1·4) implies a weighted form of Conjecture 1, namely,
Using Conjecture 1, one may prove the following two theorems. In both,
![]() $\{x\}$
denotes the fractional part of x.
$\{x\}$
denotes the fractional part of x.
Theorem 1·3. Assume the Riemann hypothesis and Conjecture 1. If
![]() $[\alpha,\beta]$
is a subinterval of [0,1], then
$[\alpha,\beta]$
is a subinterval of [0,1], then
 \begin{equation}\sup_{{\alpha}, {\beta}}\ \left| \; \sum_{ \substack{0<{\gamma } \leq T \\ \{ {\gamma } (\!\log T)/2\pi\} \in [\alpha,\beta]}} 1\ - \ (\beta-\alpha) N(T)\right|=o(N (T)).\end{equation}
\begin{equation}\sup_{{\alpha}, {\beta}}\ \left| \; \sum_{ \substack{0<{\gamma } \leq T \\ \{ {\gamma } (\!\log T)/2\pi\} \in [\alpha,\beta]}} 1\ - \ (\beta-\alpha) N(T)\right|=o(N (T)).\end{equation}
Theorem 1·4. Assume the Riemann hypothesis, Hypothesis
![]() $\mathscr{H}_{\delta}$
for some
$\mathscr{H}_{\delta}$
for some
![]() $0<{\delta}\leq 1$
, and Conjecture 1. Let a and b be either fixed, or functions of T for which
$0<{\delta}\leq 1$
, and Conjecture 1. Let a and b be either fixed, or functions of T for which
![]() $\max(|a|, |b|)\ll (\!\log \log \log T)^{\frac12-{\epsilon}}$
, where
$\max(|a|, |b|)\ll (\!\log \log \log T)^{\frac12-{\epsilon}}$
, where
![]() ${\epsilon}>0$
, and
${\epsilon}>0$
, and
![]() $\int_a^b e^{-x^2/2} dx \gg 1$
. Then if
$\int_a^b e^{-x^2/2} dx \gg 1$
. Then if
![]() $[\alpha,\beta]$
is a subinterval of [0,1],
$[\alpha,\beta]$
is a subinterval of [0,1],
 \begin{equation}\sup_{{\alpha}, {\beta}}\ \left| \; \sum_{\substack{0<{\gamma } \leq T, \,{\gamma }\in {\Gamma }_{[a, b]} \\ \{ {\gamma } (\!\log T)/2\pi\} \in [\alpha,\beta]}} 1\ - \ (\beta-\alpha) N_{[a, b]}(T)\right|=o(N_{[a, b]}(T)).\end{equation}
\begin{equation}\sup_{{\alpha}, {\beta}}\ \left| \; \sum_{\substack{0<{\gamma } \leq T, \,{\gamma }\in {\Gamma }_{[a, b]} \\ \{ {\gamma } (\!\log T)/2\pi\} \in [\alpha,\beta]}} 1\ - \ (\beta-\alpha) N_{[a, b]}(T)\right|=o(N_{[a, b]}(T)).\end{equation}
This also holds with
![]() $ {\Gamma }_{[a, b]}$
replaced by
$ {\Gamma }_{[a, b]}$
replaced by
![]() $ {\Gamma }_{[a, b]}^*$
.
$ {\Gamma }_{[a, b]}^*$
.
The method we use to prove Theorems 1·1, 1·2 and 1·4 builds on techniques used in the first author’s recent thesis to prove a discrete analogue of Selberg’s central limit theorem (see [ Reference Çiçek2 ] and Lemma 2·1 below).
Throughout we write
![]() $e(u)= e^{2\pi i u}$
. We let C denote a positive constant that may be different at different occurrences, and we let
$e(u)= e^{2\pi i u}$
. We let C denote a positive constant that may be different at different occurrences, and we let
![]() $\unicode{x1D7D9}_{[a,b]} $
denote the indicator function of the interval [a, b].
$\unicode{x1D7D9}_{[a,b]} $
denote the indicator function of the interval [a, b].
2. Proof of Theorem 1·1
Theorem 1·1 follows easily from the next lemma.
Lemma 2·1. Assume the Riemann hypothesis and that Hypothesis
![]() $\mathscr{H}_{\delta}$
holds for some
$\mathscr{H}_{\delta}$
holds for some
![]() ${\delta}\in(0, 1]$
. Let
${\delta}\in(0, 1]$
. Let
![]() $m_{\gamma }$
denote the multiplicity of the zero
$m_{\gamma }$
denote the multiplicity of the zero
![]() ${\rho }=1/2+i{\gamma }$
. Then for all sufficiently large T,
${\rho }=1/2+i{\gamma }$
. Then for all sufficiently large T,
 \begin{equation}\begin{split} \# \bigg\{ 0<{\gamma }\leq T \, :\, & \frac{ \log(\big| \zeta^{(m_{\gamma })} (\frac12+ i{\gamma }) \big| / (\!\log{T} )^{m_{\gamma }})}{\sqrt{\frac12\log\log T}} \in [a, b] \bigg\} \\=& \frac{ N(T)}{\sqrt{2\pi} } \int_a^b e^{-{x^2}/{2}} \, dx +O\bigg( N(T)\frac{(\!\log\log\log T)^2}{\sqrt{\log\log T}} \bigg) .\end{split}\end{equation}
\begin{equation}\begin{split} \# \bigg\{ 0<{\gamma }\leq T \, :\, & \frac{ \log(\big| \zeta^{(m_{\gamma })} (\frac12+ i{\gamma }) \big| / (\!\log{T} )^{m_{\gamma }})}{\sqrt{\frac12\log\log T}} \in [a, b] \bigg\} \\=& \frac{ N(T)}{\sqrt{2\pi} } \int_a^b e^{-{x^2}/{2}} \, dx +O\bigg( N(T)\frac{(\!\log\log\log T)^2}{\sqrt{\log\log T}} \bigg) .\end{split}\end{equation}
This follows from the proof of Theorem 1·4 combined with corollary 2·3 of Çiçek [ Reference Çiçek2 ].
Note that
 \begin{equation}\notag N_{[a, b]}(T)= \sum_{0 < {\gamma } \leq T} \unicode{x1D7D9}_{[a,b]}\Bigg(\frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log {\gamma })^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log {\gamma }}}\Bigg).\end{equation}
\begin{equation}\notag N_{[a, b]}(T)= \sum_{0 < {\gamma } \leq T} \unicode{x1D7D9}_{[a,b]}\Bigg(\frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log {\gamma })^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log {\gamma }}}\Bigg).\end{equation}
Thus, to prove (1·2), we need to show that we may replace
![]() $\log {\gamma }$
and
$\log {\gamma }$
and
![]() $\log\log {\gamma }$
here by
$\log\log {\gamma }$
here by
![]() $\log T$
and
$\log T$
and
![]() $\log\log T$
, respectively, at the cost of a reasonable error term. To see this, note that by (1·1), the terms in the sum with
$\log\log T$
, respectively, at the cost of a reasonable error term. To see this, note that by (1·1), the terms in the sum with
![]() $0 <{\gamma }\leq T/\log T$
contribute at most O(T), hence
$0 <{\gamma }\leq T/\log T$
contribute at most O(T), hence
 \begin{equation}N_{[a, b]}(T) = \sum_{T/\log T < {\gamma } \leq T} \unicode{x1D7D9}_{[a,b]}\Bigg(\frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log {\gamma })^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log {\gamma }}}\Bigg)+O(T).\end{equation}
\begin{equation}N_{[a, b]}(T) = \sum_{T/\log T < {\gamma } \leq T} \unicode{x1D7D9}_{[a,b]}\Bigg(\frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log {\gamma })^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log {\gamma }}}\Bigg)+O(T).\end{equation}
For
![]() $T/\log T < {\gamma } \leq T$
we easily find that
$T/\log T < {\gamma } \leq T$
we easily find that
 \begin{equation}\notag \begin{split} \frac{\log\! \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log {\gamma })^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log {\gamma }} }= &\frac{ \log\! \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log T)^{m_{\gamma }} \big)\! +O(m_{\gamma } \log\log T/ \log T) }{\sqrt{\frac12\log\log T} }\\ &\hskip1in \times\bigg(1 + O\Big(\frac{1}{\log T }\Big) \bigg).\end{split}\end{equation}
\begin{equation}\notag \begin{split} \frac{\log\! \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log {\gamma })^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log {\gamma }} }= &\frac{ \log\! \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log T)^{m_{\gamma }} \big)\! +O(m_{\gamma } \log\log T/ \log T) }{\sqrt{\frac12\log\log T} }\\ &\hskip1in \times\bigg(1 + O\Big(\frac{1}{\log T }\Big) \bigg).\end{split}\end{equation}
Using (1·1) again, we see that
![]() $m_{\gamma }\ll \log T/\log\log T$
. Thus, if we impose the condition that
$m_{\gamma }\ll \log T/\log\log T$
. Thus, if we impose the condition that
![]() $\max(|a|, |b|)\ll (\!\log \log \log T)^{\frac12-{\epsilon}}$
, then when the expression on the left lies in the interval [a, b], the right-hand side equals
$\max(|a|, |b|)\ll (\!\log \log \log T)^{\frac12-{\epsilon}}$
, then when the expression on the left lies in the interval [a, b], the right-hand side equals
 \begin{equation*} \frac{ \log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log T)^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log T} }+ O\Big(\frac{1}{ \sqrt{\log\log T} } \Big). \end{equation*}
\begin{equation*} \frac{ \log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log T)^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log T} }+ O\Big(\frac{1}{ \sqrt{\log\log T} } \Big). \end{equation*}
Using this with (2·1), we see that replacing
![]() $\log {\gamma }$
and
$\log {\gamma }$
and
![]() $\log\log {\gamma }$
in (2·2) by
$\log\log {\gamma }$
in (2·2) by
![]() $\log T$
and
$\log T$
and
![]() $\log\log T$
, respectively, changes (2·2) by no more than
$\log\log T$
, respectively, changes (2·2) by no more than
![]() $\displaystyle O( N(T) {(\!\log\log\log T)^2}/{\sqrt{\log \log T} }).$
Hence
$\displaystyle O( N(T) {(\!\log\log\log T)^2}/{\sqrt{\log \log T} }).$
Hence
 \begin{align*}\notag N_{[a, b]}(T) = & \sum_{T/\log T < {\gamma } \leq T} \unicode{x1D7D9}_{[a,b]}\Bigg(\frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log T)^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log T}}\Bigg)\\&+O\Bigg(N(T)\frac{(\!\log\log\log T)^2}{\sqrt{\log \log T} }\Bigg).\end{align*}
\begin{align*}\notag N_{[a, b]}(T) = & \sum_{T/\log T < {\gamma } \leq T} \unicode{x1D7D9}_{[a,b]}\Bigg(\frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log T)^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log T}}\Bigg)\\&+O\Bigg(N(T)\frac{(\!\log\log\log T)^2}{\sqrt{\log \log T} }\Bigg).\end{align*}
Extending the sum back to the full range
![]() $0<{\gamma }\leq T$
and using (2·1) again, we see that for sufficiently large T,
$0<{\gamma }\leq T$
and using (2·1) again, we see that for sufficiently large T,
 \begin{equation}\notag N_{[a, b]}(T) =\frac{N(T)}{\sqrt{2\pi} } \int_a^b e^{-{x^2}/{2}}\, dx +O\Bigg( N(T)\frac{(\!\log\log\log T)^2}{\sqrt{\log \log T} }\Bigg),\end{equation}
\begin{equation}\notag N_{[a, b]}(T) =\frac{N(T)}{\sqrt{2\pi} } \int_a^b e^{-{x^2}/{2}}\, dx +O\Bigg( N(T)\frac{(\!\log\log\log T)^2}{\sqrt{\log \log T} }\Bigg),\end{equation}
provided
![]() $\max(|a|, |b|)\ll (\!\log \log \log T)^{\frac12-{\epsilon}}$
. This proves (1·2). It has already been noted that (1·3) follows from (1·2) and Hypothesis
$\max(|a|, |b|)\ll (\!\log \log \log T)^{\frac12-{\epsilon}}$
. This proves (1·2). It has already been noted that (1·3) follows from (1·2) and Hypothesis
![]() $\mathscr{H}_{\delta}$
, so the proof of Theorem 1·1 is complete.
$\mathscr{H}_{\delta}$
, so the proof of Theorem 1·1 is complete.
3. Proof of Theorem 1·2
We assume the Riemann hypothesis, Hypothesis
![]() $\mathscr{H}_{\delta}$
, and that
$\mathscr{H}_{\delta}$
, and that
Our assumption that a and b are either fixed, or functions of T for which
![]() $\int_a^b e^{-x^2/2} dx \gg 1$
means, by Theorem 1·1, that
$\int_a^b e^{-x^2/2} dx \gg 1$
means, by Theorem 1·1, that
![]() $N_{[a, b]}(T) \gg N(T)$
. Hence, by Weyl’s criterion [
Reference Weyl10
], the sequence
$N_{[a, b]}(T) \gg N(T)$
. Hence, by Weyl’s criterion [
Reference Weyl10
], the sequence
![]() $ {\Gamma }_{[a, b]}$
is uniformly distributed modulo one if, for each fixed positive integer
$ {\Gamma }_{[a, b]}$
is uniformly distributed modulo one if, for each fixed positive integer
![]() $\ell$
,
$\ell$
,
 \begin{equation} \sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) \,\, \unicode{x1D7D9}_{[a,b]}\Bigg(\frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log {\gamma })^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log {\gamma }}}\Bigg)=o(N(T))\end{equation}
\begin{equation} \sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) \,\, \unicode{x1D7D9}_{[a,b]}\Bigg(\frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log {\gamma })^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log {\gamma }}}\Bigg)=o(N(T))\end{equation}
as
![]() $T\to\infty$
. By the same argument we used in the last section, replacing
$T\to\infty$
. By the same argument we used in the last section, replacing
![]() $\log {\gamma }$
and
$\log {\gamma }$
and
![]() $\log\log {\gamma }$
here by
$\log\log {\gamma }$
here by
![]() $\log T$
and
$\log T$
and
![]() $\log\log T$
, respectively, changes the sum by at most o(N(T). Thus, it suffices to show that
$\log\log T$
, respectively, changes the sum by at most o(N(T). Thus, it suffices to show that
 \begin{equation}\notag \begin{split} \sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) \,\, \unicode{x1D7D9}_{[a,b]}\Bigg( \frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log T)^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log T}}\Bigg) = o( N(T)).\end{split}\end{equation}
\begin{equation}\notag \begin{split} \sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) \,\, \unicode{x1D7D9}_{[a,b]}\Bigg( \frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log T)^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log T}}\Bigg) = o( N(T)).\end{split}\end{equation}
Now let
 $ \displaystyle P({\gamma }) =\sum_{p \leq X^2} \frac{1}{ p^{1/2+i{\gamma }} },$
where p runs over the primes. The gist of corollary 2·3 in [
Reference Çiçek2
] and some of the analysis following it, is that
$ \displaystyle P({\gamma }) =\sum_{p \leq X^2} \frac{1}{ p^{1/2+i{\gamma }} },$
where p runs over the primes. The gist of corollary 2·3 in [
Reference Çiçek2
] and some of the analysis following it, is that
![]() $P({\gamma })$
is on average a good approximation to
$P({\gamma })$
is on average a good approximation to
 \begin{equation*} \frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log T)^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log T}}, \end{equation*}
\begin{equation*} \frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log T)^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log T}}, \end{equation*}
provided X is sufficiently large. Indeed, from the discussion in sections 5·5 and 6 of [ Reference Çiçek2 ] it follows that
 \begin{align*}\sum_{0<{\gamma } \leq T}\unicode{x1D7D9}_{[a,b]}\Bigg( \frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log T)^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log T}} \Bigg)= \sum_{0<{\gamma } \leq T} & \unicode{x1D7D9}_{[a,b]} \Bigg(\frac{\Re {P({\gamma })}}{\sqrt{\frac12\log\log T}}\Bigg) \\ &+O \bigg(N(T) \frac{(\!\log\log\log T)^2}{\sqrt{\log\log T}} \bigg). \end{align*}
\begin{align*}\sum_{0<{\gamma } \leq T}\unicode{x1D7D9}_{[a,b]}\Bigg( \frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log T)^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log T}} \Bigg)= \sum_{0<{\gamma } \leq T} & \unicode{x1D7D9}_{[a,b]} \Bigg(\frac{\Re {P({\gamma })}}{\sqrt{\frac12\log\log T}}\Bigg) \\ &+O \bigg(N(T) \frac{(\!\log\log\log T)^2}{\sqrt{\log\log T}} \bigg). \end{align*}
This is the key result that allows us to prove our theorem. An immediate consequence is that
 \begin{equation*}\unicode{x1D7D9}_{[a,b]} \Bigg(\frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log T)^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log T}}\Bigg)= \unicode{x1D7D9}_{[a,b]} \Bigg(\frac{\Re{P({\gamma })}}{\sqrt{\frac12\log\log T}}\Bigg)\end{equation*}
\begin{equation*}\unicode{x1D7D9}_{[a,b]} \Bigg(\frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log T)^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log T}}\Bigg)= \unicode{x1D7D9}_{[a,b]} \Bigg(\frac{\Re{P({\gamma })}}{\sqrt{\frac12\log\log T}}\Bigg)\end{equation*}
for all but
![]() $\displaystyle O\big(N(T) (\!\log\log\log T)^2/\sqrt{\log\log T} \big)=o(N(T))$
values of
$\displaystyle O\big(N(T) (\!\log\log\log T)^2/\sqrt{\log\log T} \big)=o(N(T))$
values of
![]() ${\gamma }$
in (0, T]. Therefore,
${\gamma }$
in (0, T]. Therefore,
 \begin{equation}\begin{split} \sum_{0<{\gamma } \leq T} & e(\ell{\gamma }) \unicode{x1D7D9}_{[a,b]} \Bigg(\frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log T)^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log T}}\Bigg) \\=& \sum_{0<{\gamma } \leq T} e(\ell{\gamma }) \unicode{x1D7D9}_{[a,b]} \Bigg(\frac{\Re P({\gamma })}{\sqrt{\frac12\log\log T}}\Bigg)+ O \bigg(N(T) \frac{(\!\log\log\log T)^2}{\sqrt{\log\log T}} \bigg).\end{split}\end{equation}
\begin{equation}\begin{split} \sum_{0<{\gamma } \leq T} & e(\ell{\gamma }) \unicode{x1D7D9}_{[a,b]} \Bigg(\frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log T)^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log T}}\Bigg) \\=& \sum_{0<{\gamma } \leq T} e(\ell{\gamma }) \unicode{x1D7D9}_{[a,b]} \Bigg(\frac{\Re P({\gamma })}{\sqrt{\frac12\log\log T}}\Bigg)+ O \bigg(N(T) \frac{(\!\log\log\log T)^2}{\sqrt{\log\log T}} \bigg).\end{split}\end{equation}
Writing
we see that to prove our theorem we must show that
for each positive integer
![]() $\ell$
. To do this, we replace the characteristic function
$\ell$
. To do this, we replace the characteristic function
![]() $\unicode{x1D7D9}_{[A, B]}$
by an approximation. Let
$\unicode{x1D7D9}_{[A, B]}$
by an approximation. Let
![]() $\Omega > 0$
and set
$\Omega > 0$
and set
where
Then
(see [ Reference Tsang9 , pp. 26–29]). It follows that
This is the desired approximation of
![]() $ \unicode{x1D7D9}_{[A, B]}$
. Here we take
$ \unicode{x1D7D9}_{[A, B]}$
. Here we take
 $\displaystyle x=\Re{ {P}({\gamma })} = \Re \sum_{p \leq X^2} \frac{1}{ p^{1/2+i{\gamma }} }$
and
$\displaystyle x=\Re{ {P}({\gamma })} = \Re \sum_{p \leq X^2} \frac{1}{ p^{1/2+i{\gamma }} }$
and
Now, it was shown in the course of the proof of proposition 5·5 in [ Reference Çiçek2 ] (with slightly different notation and parameters) that
 \begin{equation}\notag \sum_{0 < {\gamma } \leq T}\frac{\sin^2\big(\pi \Omega(\Re {P}({\gamma })-A)\big)}{\big(\pi \Omega(\Re {P}({\gamma })-A)\big)^2} \ll \frac{N(T)}{\Omega},\end{equation}
\begin{equation}\notag \sum_{0 < {\gamma } \leq T}\frac{\sin^2\big(\pi \Omega(\Re {P}({\gamma })-A)\big)}{\big(\pi \Omega(\Re {P}({\gamma })-A)\big)^2} \ll \frac{N(T)}{\Omega},\end{equation}
and similarly for the sum with A replaced by B. Thus, by (3·6),
 \begin{equation}\begin{split}& \sum_{0<{\gamma } \leq T}e(\ell{\gamma }) \unicode{x1D7D9}_{[A, B]} ( \Re {P}({\gamma })) \\ = &\, \frac{1}{2} \sum_{0<{\gamma } \leq T} e(\ell{\gamma }) F_{\Omega} (\Re{ P({\gamma })}-A)-\frac{1}{2} \sum_{0<{\gamma } \leq T} e(\ell{\gamma }) F_{\Omega}(\Re {P}({\gamma })-B)+O\Big( \frac{N(T)}{\Omega}\Big) .\end{split}\end{equation}
\begin{equation}\begin{split}& \sum_{0<{\gamma } \leq T}e(\ell{\gamma }) \unicode{x1D7D9}_{[A, B]} ( \Re {P}({\gamma })) \\ = &\, \frac{1}{2} \sum_{0<{\gamma } \leq T} e(\ell{\gamma }) F_{\Omega} (\Re{ P({\gamma })}-A)-\frac{1}{2} \sum_{0<{\gamma } \leq T} e(\ell{\gamma }) F_{\Omega}(\Re {P}({\gamma })-B)+O\Big( \frac{N(T)}{\Omega}\Big) .\end{split}\end{equation}
From this and (3·3) we see that it suffices to prove that
for each positive integer
![]() $\ell$
, and similarly for the sum with A replaced by B.
$\ell$
, and similarly for the sum with A replaced by B.
To this end we use (3·4) to write
 \begin{align} \sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) F_{\Omega}(\Re {P}({\gamma })-A) =\sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) \Im \int_0^\Omega G\Big(\frac \omega \Omega\Big) e^{-2\pi i A \omega} \exp{\big(2\pi i\omega\Re {P}({\gamma }) \big)}\frac{\mathop{d\omega}}{\omega}. \end{align}
\begin{align} \sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) F_{\Omega}(\Re {P}({\gamma })-A) =\sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) \Im \int_0^\Omega G\Big(\frac \omega \Omega\Big) e^{-2\pi i A \omega} \exp{\big(2\pi i\omega\Re {P}({\gamma }) \big)}\frac{\mathop{d\omega}}{\omega}. \end{align}
By Taylor’s theorem, for any positive integer K,
 \begin{equation}\notag \exp\big(2\pi i\omega\Re{P}({\gamma })\big) =1+\sum_{1\leq k < K} \frac{(2\pi i\omega\Re {P}({\gamma }))^k}{k!} + O\Big(\frac{(2\pi \omega|\Re {P}({\gamma })|)^K}{K!}\Big). \end{equation}
\begin{equation}\notag \exp\big(2\pi i\omega\Re{P}({\gamma })\big) =1+\sum_{1\leq k < K} \frac{(2\pi i\omega\Re {P}({\gamma }))^k}{k!} + O\Big(\frac{(2\pi \omega|\Re {P}({\gamma })|)^K}{K!}\Big). \end{equation}
Inserting this in (3·10) and taking
where [x] denotes the greatest integer less than or equal to x, we obtain
 \begin{align} \notag \sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) F_{\Omega}(\Re {P}({\gamma })-A) =&\, F_\Omega(A) \sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) \\ +\sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) \Im \int_0^\Omega & G\Big(\frac \omega \Omega\Big) e^{-2\pi i A \omega} \sum_{1\leq k < K}\frac{(2\pi i\omega)^k}{k!} (\Re {P}({\gamma }))^k \frac{\mathop{d\omega}}{\omega}\\ \notag &+ O\bigg( \sum_{0 < {\gamma } \leq T} |\Re {P}({\gamma })|^K \int_0^\Omega G\Big(\frac \omega \Omega\Big) \frac{(2\pi\omega)^K}{K!} \frac{\mathop{d\omega}}{\omega} \bigg). \end{align}
\begin{align} \notag \sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) F_{\Omega}(\Re {P}({\gamma })-A) =&\, F_\Omega(A) \sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) \\ +\sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) \Im \int_0^\Omega & G\Big(\frac \omega \Omega\Big) e^{-2\pi i A \omega} \sum_{1\leq k < K}\frac{(2\pi i\omega)^k}{k!} (\Re {P}({\gamma }))^k \frac{\mathop{d\omega}}{\omega}\\ \notag &+ O\bigg( \sum_{0 < {\gamma } \leq T} |\Re {P}({\gamma })|^K \int_0^\Omega G\Big(\frac \omega \Omega\Big) \frac{(2\pi\omega)^K}{K!} \frac{\mathop{d\omega}}{\omega} \bigg). \end{align}
We estimate the sums over
![]() ${\gamma }$
on the right-hand side of the equation by means of the following result, which is an immediate consequence of an unconditional theorem and its corollary in [
Reference Gonek5
] (see [
Reference Gonek4
] also).
${\gamma }$
on the right-hand side of the equation by means of the following result, which is an immediate consequence of an unconditional theorem and its corollary in [
Reference Gonek5
] (see [
Reference Gonek4
] also).
Lemma 3·1. Assume the Riemann hypothesis and let
![]() $x, T>1$
. Then
$x, T>1$
. Then
 \begin{equation} \begin{split} \sum_{0<{\gamma }\leq T} x^{i{\gamma }}= - &\frac{T}{2\pi}\frac{\Lambda(x)}{\sqrt x} +O(\sqrt{x} \log 2xT \log\log 3x) +O\Big(\!\log x\min\Big(\frac{T}{\sqrt x}, \frac{\sqrt x}{\langle x \rangle}\Big)\Big) \\ &+O\Big(\!\log 2T \min\Big(\frac{T}{\sqrt x}, \frac{1}{\sqrt x \log x} \Big)\Big). \end{split} \end{equation}
\begin{equation} \begin{split} \sum_{0<{\gamma }\leq T} x^{i{\gamma }}= - &\frac{T}{2\pi}\frac{\Lambda(x)}{\sqrt x} +O(\sqrt{x} \log 2xT \log\log 3x) +O\Big(\!\log x\min\Big(\frac{T}{\sqrt x}, \frac{\sqrt x}{\langle x \rangle}\Big)\Big) \\ &+O\Big(\!\log 2T \min\Big(\frac{T}{\sqrt x}, \frac{1}{\sqrt x \log x} \Big)\Big). \end{split} \end{equation}
Here
![]() $\Lambda(x)=\log p$
if x is a positive integral power of a prime p and
$\Lambda(x)=\log p$
if x is a positive integral power of a prime p and
![]() $\Lambda(x)=0$
for all other real numbers x, and
$\Lambda(x)=0$
for all other real numbers x, and
![]() $\langle x\rangle$
denotes the distance from x to the nearest prime power other than x itself. If
$\langle x\rangle$
denotes the distance from x to the nearest prime power other than x itself. If
![]() $0<x<1$
, (3·13) also holds provided we replace x on the right-hand side by
$0<x<1$
, (3·13) also holds provided we replace x on the right-hand side by
![]() $1/x$
.
$1/x$
.
When
![]() $x>1$
, we will write (3·13) as
$x>1$
, we will write (3·13) as
where M(x) and
![]() $E_i(x), \ i=1, 2, 3,$
also depend on T. When
$E_i(x), \ i=1, 2, 3,$
also depend on T. When
![]() $0<x<1$
, all the x’s on the right-hand side of (3·14) are to be replaced by
$0<x<1$
, all the x’s on the right-hand side of (3·14) are to be replaced by
![]() $1/x$
. Note that when
$1/x$
. Note that when
![]() $x=1$
,
$x=1$
,
![]() $ \sum_{0<{\gamma }\leq T} x^{i{\gamma }}=N(T)$
.
$ \sum_{0<{\gamma }\leq T} x^{i{\gamma }}=N(T)$
.
Returning to (3·12), observe that by (3·5),
![]() $F_{\Omega}(A) \ll 1$
. Furthermore, taking
$F_{\Omega}(A) \ll 1$
. Furthermore, taking
![]() $x=e^{2\pi \ell }>1$
in (3·13), we find that
$x=e^{2\pi \ell }>1$
in (3·13), we find that
![]() $\sum_{0<{\gamma }\leq T}e(\ell {\gamma }) \ll T$
. Thus, the first term on the right-hand side of (3·12) is
$\sum_{0<{\gamma }\leq T}e(\ell {\gamma }) \ll T$
. Thus, the first term on the right-hand side of (3·12) is
For the final term in (3·12) we use lemma 5·2 of [ Reference Çiçek2 ], which says that
where
![]() $ \Psi =\log\log T.$
From this and Stirling’s approximation, we find that the O-term in (3·12) is
$ \Psi =\log\log T.$
From this and Stirling’s approximation, we find that the O-term in (3·12) is
 \begin{align*} &\ll N(T) \int_0^\Omega G\Big(\frac \omega \Omega\Big) \frac{(2\pi \omega)^K}{K!}(cK\Psi)^{K/2} \frac{\mathop{d\omega}}{\omega} \\ &\ll N(T) \int_0^\Omega G\Big(\frac \omega \Omega\Big) \frac{\omega(2\pi e)^K\omega^{K-1}}{K^K} (cK\Psi)^{K/2} \frac{\mathop{d\omega}}{\omega}. \end{align*}
\begin{align*} &\ll N(T) \int_0^\Omega G\Big(\frac \omega \Omega\Big) \frac{(2\pi \omega)^K}{K!}(cK\Psi)^{K/2} \frac{\mathop{d\omega}}{\omega} \\ &\ll N(T) \int_0^\Omega G\Big(\frac \omega \Omega\Big) \frac{\omega(2\pi e)^K\omega^{K-1}}{K^K} (cK\Psi)^{K/2} \frac{\mathop{d\omega}}{\omega}. \end{align*}
By (3·7) and (3·11), and since G is bounded, this is
Combining this and (3·15), we may rewrite (3·12) as
 \begin{equation} \begin{split} & \sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) F_{\Omega}(\Re P({\gamma })-A) \\ =& \int_0^\Omega G\Big(\frac \omega \Omega\Big) \sum_{1\leq k < K} \Im{\big(e^{-2\pi i A \omega}\, i^k\big)} \frac{(2\pi\omega)^k}{k!} \sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) (\Re P({\gamma }))^k \frac{\mathop{d\omega}}{\omega} +O(T). \end{split} \end{equation}
\begin{equation} \begin{split} & \sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) F_{\Omega}(\Re P({\gamma })-A) \\ =& \int_0^\Omega G\Big(\frac \omega \Omega\Big) \sum_{1\leq k < K} \Im{\big(e^{-2\pi i A \omega}\, i^k\big)} \frac{(2\pi\omega)^k}{k!} \sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) (\Re P({\gamma }))^k \frac{\mathop{d\omega}}{\omega} +O(T). \end{split} \end{equation}
To estimate the right-hand side we next bound the sums
By the binomial theorem
 \begin{equation*} S(k) = \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) \Bigg(\sum_{p\leq X^2}\frac{1}{p^{1/2+i{\gamma }}}\Bigg)^j \Bigg(\sum_{p\leq X^2}\frac{1}{p^{1/2-i{\gamma }}}\Bigg)^{k-j}. \end{equation*}
\begin{equation*} S(k) = \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) \Bigg(\sum_{p\leq X^2}\frac{1}{p^{1/2+i{\gamma }}}\Bigg)^j \Bigg(\sum_{p\leq X^2}\frac{1}{p^{1/2-i{\gamma }}}\Bigg)^{k-j}. \end{equation*}
Let
![]() $a_{r}(p_1\dots p_{r})$
denote the number of permutations of the primes
$a_{r}(p_1\dots p_{r})$
denote the number of permutations of the primes
![]() $p_1,\dots, p_{r}$
, which might or might not be distinct. Also, for the rest of the paper, n will always denote a product of j primes, each of which is at most
$p_1,\dots, p_{r}$
, which might or might not be distinct. Also, for the rest of the paper, n will always denote a product of j primes, each of which is at most
![]() $X^2$
, while m denotes a product of
$X^2$
, while m denotes a product of
![]() $k-j$
primes, again each of size at most
$k-j$
primes, again each of size at most
![]() $X^2$
. We may thus write
$X^2$
. We may thus write
 \begin{align*} S(k) =&\, \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) \sum_n \frac{a_j(n)}{n^{1/2+i{\gamma }}} \sum_m \frac{a_{k-j}(m)}{m^{1/2-i{\gamma }}} \\ =&\,\frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{\sqrt n} \sum_m \frac{a_{k-j}(m)}{\sqrt m} \sum_{0 < {\gamma } \leq T} \Big(\frac{m e^{2\pi\ell}}{n}\Big)^{i{\gamma }}. \end{align*}
\begin{align*} S(k) =&\, \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) \sum_n \frac{a_j(n)}{n^{1/2+i{\gamma }}} \sum_m \frac{a_{k-j}(m)}{m^{1/2-i{\gamma }}} \\ =&\,\frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{\sqrt n} \sum_m \frac{a_{k-j}(m)}{\sqrt m} \sum_{0 < {\gamma } \leq T} \Big(\frac{m e^{2\pi\ell}}{n}\Big)^{i{\gamma }}. \end{align*}
Since
![]() $e^{2\pi \ell} = ({-}1)^{-2i\ell}$
is of the form
$e^{2\pi \ell} = ({-}1)^{-2i\ell}$
is of the form
![]() ${\alpha} _0^{{\beta}_0}$
with
${\alpha} _0^{{\beta}_0}$
with
![]() ${\alpha} _0, {\beta}_0$
algebraic,
${\alpha} _0, {\beta}_0$
algebraic,
![]() ${\alpha} _0\neq 0,1$
and
${\alpha} _0\neq 0,1$
and
![]() $-2i\ell$
not rational, the Gelfond–Schneider theorem implies that
$-2i\ell$
not rational, the Gelfond–Schneider theorem implies that
![]() $e^{2\pi \ell}$
is transcendental. Thus,
$e^{2\pi \ell}$
is transcendental. Thus,
![]() $m e^{2\pi\ell}/{n}$
can neither be a positive integer nor the reciprocal of a positive integer. The M term in integer. The M term in (3·14) is therefore always zero. Hence, we may write
$m e^{2\pi\ell}/{n}$
can neither be a positive integer nor the reciprocal of a positive integer. The M term in integer. The M term in (3·14) is therefore always zero. Hence, we may write
 \begin{equation} \begin{split}S(k) &= \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{\sqrt n} \sum_{\substack{m\\{me^{2\pi\ell}}/{n} >1}} \frac{a_{k-j}(m)}{\sqrt m} \bigg( \sum_{i=1}^3 E_i \Big(\frac{m e^{2\pi\ell}}{n}\Big)\bigg)\\ &\quad + \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{\sqrt n} \sum_{\substack{m\\{me^{2\pi\ell}}/{n} <1}} \frac{a_{k-j}(m)}{\sqrt m} \bigg( \sum_{i=1}^3 E_i \Big(\frac{n}{m e^{2\pi\ell}}\Big)\bigg) \\& \,=\!:\, S_1(k) + S_2(k). \end{split} \end{equation}
\begin{equation} \begin{split}S(k) &= \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{\sqrt n} \sum_{\substack{m\\{me^{2\pi\ell}}/{n} >1}} \frac{a_{k-j}(m)}{\sqrt m} \bigg( \sum_{i=1}^3 E_i \Big(\frac{m e^{2\pi\ell}}{n}\Big)\bigg)\\ &\quad + \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{\sqrt n} \sum_{\substack{m\\{me^{2\pi\ell}}/{n} <1}} \frac{a_{k-j}(m)}{\sqrt m} \bigg( \sum_{i=1}^3 E_i \Big(\frac{n}{m e^{2\pi\ell}}\Big)\bigg) \\& \,=\!:\, S_1(k) + S_2(k). \end{split} \end{equation}
To estimate
![]() $S_1(k)$
, we insert the bounds for
$S_1(k)$
, we insert the bounds for
![]() $E_1, E_2,$
and
$E_1, E_2,$
and
![]() $E_3$
from (3·13) in to obtain
$E_3$
from (3·13) in to obtain
where
 \begin{equation}\notag \begin{split} \mathcal E_1(k)&= \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{\sqrt n} \sum_{\substack{m\\{me^{2\pi\ell}}/{n} >1}} \frac{a_{k-j}(m)}{\sqrt m} \sqrt{\frac{me^{2\pi \ell}}{n}} \log\Big(\frac{me^{2\pi \ell}T}{n}\Big) \log\log\Big(\frac{3me^{2\pi \ell}}{n}\Big), \\ \mathcal E_2(k)&= \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{\sqrt n} \sum_{\substack{m\\{me^{2\pi\ell}}/{n} >1}} \frac{a_{k-j}(m)}{\sqrt m} \frac{ \log(me^{2\pi \ell}/n)}{\sqrt{me^{2\pi \ell}/n}} \min\bigg(T, \frac{me^{2\pi \ell}/n }{\langle me^{2\pi \ell}/n \rangle} \bigg), \\ \mathcal E_3(k)&= \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{\sqrt n} \sum_{\substack{m\\{me^{2\pi\ell}}/{n} >1}} \frac{a_{k-j}(m)}{\sqrt m} \frac{\log T}{\sqrt{me^{2\pi \ell}/n} } \min \bigg(T, \frac{ 1}{\log(me^{2\pi \ell}/n)} \bigg). \end{split} \end{equation}
\begin{equation}\notag \begin{split} \mathcal E_1(k)&= \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{\sqrt n} \sum_{\substack{m\\{me^{2\pi\ell}}/{n} >1}} \frac{a_{k-j}(m)}{\sqrt m} \sqrt{\frac{me^{2\pi \ell}}{n}} \log\Big(\frac{me^{2\pi \ell}T}{n}\Big) \log\log\Big(\frac{3me^{2\pi \ell}}{n}\Big), \\ \mathcal E_2(k)&= \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{\sqrt n} \sum_{\substack{m\\{me^{2\pi\ell}}/{n} >1}} \frac{a_{k-j}(m)}{\sqrt m} \frac{ \log(me^{2\pi \ell}/n)}{\sqrt{me^{2\pi \ell}/n}} \min\bigg(T, \frac{me^{2\pi \ell}/n }{\langle me^{2\pi \ell}/n \rangle} \bigg), \\ \mathcal E_3(k)&= \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{\sqrt n} \sum_{\substack{m\\{me^{2\pi\ell}}/{n} >1}} \frac{a_{k-j}(m)}{\sqrt m} \frac{\log T}{\sqrt{me^{2\pi \ell}/n} } \min \bigg(T, \frac{ 1}{\log(me^{2\pi \ell}/n)} \bigg). \end{split} \end{equation}
First consider
![]() $\mathcal E_1(k)$
. Since
$\mathcal E_1(k)$
. Since
![]() $e^{2\pi \ell}$
is fixed, we see that
$e^{2\pi \ell}$
is fixed, we see that
 \begin{align*} \mathcal E_1(k) &= \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{n} \sum_{\substack{m\\{me^{2\pi\ell}}/{n} >1}} a_{k-j}(m) \log\Big(\frac{mT}{n}\Big) \log\log \Big(\frac{3m}{n}\Big) \\ &\ll \frac{\log T\log\log T }{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n {a_j(n)} \sum_{\substack{m\\{me^{2\pi\ell}}/{n} >1}} a_{k-j}(m). \end{align*}
\begin{align*} \mathcal E_1(k) &= \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{n} \sum_{\substack{m\\{me^{2\pi\ell}}/{n} >1}} a_{k-j}(m) \log\Big(\frac{mT}{n}\Big) \log\log \Big(\frac{3m}{n}\Big) \\ &\ll \frac{\log T\log\log T }{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n {a_j(n)} \sum_{\substack{m\\{me^{2\pi\ell}}/{n} >1}} a_{k-j}(m). \end{align*}
Here we have dropped the n in the denominator in the sum over n and used (3·7) and (3·11) to deduce that
![]() $m \leq X^{2k} \leq X^{2K} \leq T$
. Next, from the definitions of
$m \leq X^{2k} \leq X^{2K} \leq T$
. Next, from the definitions of
![]() $a_j(n)$
and
$a_j(n)$
and
![]() $a_{k-j}(m)$
and by the binomial theorem, we see that
$a_{k-j}(m)$
and by the binomial theorem, we see that
 \begin{equation} \begin{split} & \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n a_j(n) \sum_{\substack{m\\{me^{2\pi\ell}}/{n} >1}} a_{k-j}(m) \\ &\ll \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \Bigg( \sum_{p\leq X^2}1\Bigg)^j \Bigg( \sum_{p\leq X^2} 1\Bigg)^{k-j} = \pi(X^2)^k, \end{split} \end{equation}
\begin{equation} \begin{split} & \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n a_j(n) \sum_{\substack{m\\{me^{2\pi\ell}}/{n} >1}} a_{k-j}(m) \\ &\ll \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \Bigg( \sum_{p\leq X^2}1\Bigg)^j \Bigg( \sum_{p\leq X^2} 1\Bigg)^{k-j} = \pi(X^2)^k, \end{split} \end{equation}
where
![]() $\pi(X^2)$
denotes the number of primes up to
$\pi(X^2)$
denotes the number of primes up to
![]() $X^2$
. By the prime number theorem
$X^2$
. By the prime number theorem
![]() $\pi(X^2)\ll {X^{2}}/{\log X}, $
so
$\pi(X^2)\ll {X^{2}}/{\log X}, $
so
To estimate
 \begin{equation} \mathcal E_2(k)= \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{\sqrt n} \sum_{\substack{m\\{me^{2\pi\ell}}/{n} >1}} \frac{a_{k-j}(m)}{\sqrt m} \frac{ \log(me^{2\pi \ell}/n)}{\sqrt{me^{2\pi \ell}/n}} \min\bigg(T, \frac{me^{2\pi \ell}/n }{\langle me^{2\pi \ell}/n \rangle} \bigg),\end{equation}
\begin{equation} \mathcal E_2(k)= \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{\sqrt n} \sum_{\substack{m\\{me^{2\pi\ell}}/{n} >1}} \frac{a_{k-j}(m)}{\sqrt m} \frac{ \log(me^{2\pi \ell}/n)}{\sqrt{me^{2\pi \ell}/n}} \min\bigg(T, \frac{me^{2\pi \ell}/n }{\langle me^{2\pi \ell}/n \rangle} \bigg),\end{equation}
we require a lower bound for
![]() $\displaystyle \langle {me^{2\pi\ell}}/{n}\rangle$
. Recall that
$\displaystyle \langle {me^{2\pi\ell}}/{n}\rangle$
. Recall that
![]() $\langle x\rangle $
denotes the distance from x to the nearest prime power other than x itself. As
$\langle x\rangle $
denotes the distance from x to the nearest prime power other than x itself. As
![]() $e^{2\pi\ell}$
is transcendental,
$e^{2\pi\ell}$
is transcendental,
![]() $me^{2\pi \ell}/n$
is not an integer. Now, for any positive non integral real number x, we have
$me^{2\pi \ell}/n$
is not an integer. Now, for any positive non integral real number x, we have
Thus
We now recall a special case of Baker’s theorem [
Reference Baker1
, p. 24]. Since
![]() $e^{2\pi \ell} = ({-}1)^{-2i \ell}$
, for a given positive integer
$e^{2\pi \ell} = ({-}1)^{-2i \ell}$
, for a given positive integer
![]() $\ell$
,
$\ell$
,
for all rationals
![]() $p/q$
(
$p/q$
(
![]() $p\geq 0, q\geq 4$
), where C is a constant that depends on
$p\geq 0, q\geq 4$
), where C is a constant that depends on
![]() $\ell$
. Thus
$\ell$
. Thus
If we let
![]() $q=m$
and
$q=m$
and
![]() $\displaystyle p=n\Big[\frac{me^{2\pi\ell}}{n} \Big] $
, we obtain
$\displaystyle p=n\Big[\frac{me^{2\pi\ell}}{n} \Big] $
, we obtain
Similarly, taking
![]() $q=m$
and
$q=m$
and
![]() $\displaystyle p=n\Big[\frac{me^{2\pi\ell}}{n} \Big] +n$
, we see that
$\displaystyle p=n\Big[\frac{me^{2\pi\ell}}{n} \Big] +n$
, we see that
![]() $\displaystyle\Big( 1- \frac{me^{2\pi\ell}}{n} + \Big[\frac{me^{2\pi\ell}}{n} \Big] \Big)$
has the same lower bound. Hence
$\displaystyle\Big( 1- \frac{me^{2\pi\ell}}{n} + \Big[\frac{me^{2\pi\ell}}{n} \Big] \Big)$
has the same lower bound. Hence
provided
![]() $m\geq 4$
. Now the terms in (3·21) with
$m\geq 4$
. Now the terms in (3·21) with
![]() $1\leq m \leq 3$
contribute
$1\leq m \leq 3$
contribute
 \begin{equation}\notag \begin{split} & \ll_{\ell} \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_{n<6 e^{2\pi\ell}} \frac{a_j(n)}{n} \sum_{m\leq 3} a_{k-j}(m) \\ &\ll \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \Bigg(\sum_{p\leq 6 e^{2\pi\ell} }1 \Bigg)^j \Bigg(\sum_{p\leq 3}1 \Bigg)^{k-j} \ll e^{ C k},\end{split}\end{equation}
\begin{equation}\notag \begin{split} & \ll_{\ell} \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_{n<6 e^{2\pi\ell}} \frac{a_j(n)}{n} \sum_{m\leq 3} a_{k-j}(m) \\ &\ll \frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \Bigg(\sum_{p\leq 6 e^{2\pi\ell} }1 \Bigg)^j \Bigg(\sum_{p\leq 3}1 \Bigg)^{k-j} \ll e^{ C k},\end{split}\end{equation}
where C is a constant depending on
![]() $\ell$
. Using (3·23) to estimate the terms in (3·21) with
$\ell$
. Using (3·23) to estimate the terms in (3·21) with
![]() $m\geq 4$
, we find that they contribute
$m\geq 4$
, we find that they contribute
 \begin{equation}\notag \begin{split}& \ll \frac{\log T}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n a_j(n) \sum_m {a_{k-j}(m)} m^{C \log\log m} \\ & \ll\frac{\log T}{2^k} X^{3Ck \log\log X}\sum_{j=0}^k \binom{k}{j} \Bigg(\sum_{p\leq X^2 }1\Bigg)^j \Bigg(\sum_{p\leq X^2 }1\Bigg)^{k-j} \\ & \ll (\!\log T ) \pi(X^2 )^{k} X^{3Ck \log\log X} \ll (\!\log T ) X^{4Ck \log\log X}.\end{split}\end{equation}
\begin{equation}\notag \begin{split}& \ll \frac{\log T}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n a_j(n) \sum_m {a_{k-j}(m)} m^{C \log\log m} \\ & \ll\frac{\log T}{2^k} X^{3Ck \log\log X}\sum_{j=0}^k \binom{k}{j} \Bigg(\sum_{p\leq X^2 }1\Bigg)^j \Bigg(\sum_{p\leq X^2 }1\Bigg)^{k-j} \\ & \ll (\!\log T ) \pi(X^2 )^{k} X^{3Ck \log\log X} \ll (\!\log T ) X^{4Ck \log\log X}.\end{split}\end{equation}
Thus,
Next consider
 \begin{equation} \mathcal E_3(k) =\frac{\log T}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n a_j(n) \sum_{\substack{m\\{me^{2\pi\ell}}/{n} >1}} \frac{a_{k-j}(m)}{m} \min \bigg(T, \frac{ 1}{\log(me^{2\pi\ell }/n)} \bigg).\end{equation}
\begin{equation} \mathcal E_3(k) =\frac{\log T}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n a_j(n) \sum_{\substack{m\\{me^{2\pi\ell}}/{n} >1}} \frac{a_{k-j}(m)}{m} \min \bigg(T, \frac{ 1}{\log(me^{2\pi\ell }/n)} \bigg).\end{equation}
Since
![]() $m, n \leq X^{2k}$
, by (3·22) with
$m, n \leq X^{2k}$
, by (3·22) with
![]() $p=n, q=m$
and
$p=n, q=m$
and
![]() $m\geq 4$
, we have
$m\geq 4$
, we have
Thus,
for
![]() $m\geq 4$
. The terms in (3·24) with
$m\geq 4$
. The terms in (3·24) with
![]() $m\leq 3$
contribute
$m\leq 3$
contribute
 \begin{equation}\notag \begin{split}&\ll \frac{\log T}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_{n<6 e^{2\pi\ell} } a_j(n) \sum_{m\leq 3} {a_{k-j}(m)} \\&=\frac{\log T}{2^k}\sum_{j=0}^k \binom{k}{j} \Bigg(\sum_{p\leq 6 e^{2\pi\ell} }1 \Bigg)^j \Bigg(\sum_{p\leq 3}1 \Bigg)^{k-j}\ll e^{Ck} \log T.\end{split}\end{equation}
\begin{equation}\notag \begin{split}&\ll \frac{\log T}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_{n<6 e^{2\pi\ell} } a_j(n) \sum_{m\leq 3} {a_{k-j}(m)} \\&=\frac{\log T}{2^k}\sum_{j=0}^k \binom{k}{j} \Bigg(\sum_{p\leq 6 e^{2\pi\ell} }1 \Bigg)^j \Bigg(\sum_{p\leq 3}1 \Bigg)^{k-j}\ll e^{Ck} \log T.\end{split}\end{equation}
The contribution of the terms with
![]() $m\geq 4$
is
$m\geq 4$
is
 \begin{align*} \begin{split} \mathcal E_3(k) & \ll X^{3kC\log\log X} \ \frac{\log T }{2^k} \sum_{j=0}^k \binom{k}{j} \sum_n a_j(n) \sum_{m} a_{k-j}(m) \\ &=X^{3kC\log\log X} \ \pi(X^2)^k \log T \ll \frac{X^{2k} \log T}{(\!\log X)^{k}} X^{3kC\log\log X} \ll X^{4kC\log\log X} \log T. \end{split} \end{align*}
\begin{align*} \begin{split} \mathcal E_3(k) & \ll X^{3kC\log\log X} \ \frac{\log T }{2^k} \sum_{j=0}^k \binom{k}{j} \sum_n a_j(n) \sum_{m} a_{k-j}(m) \\ &=X^{3kC\log\log X} \ \pi(X^2)^k \log T \ll \frac{X^{2k} \log T}{(\!\log X)^{k}} X^{3kC\log\log X} \ll X^{4kC\log\log X} \log T. \end{split} \end{align*}
Thus
Combining our estimates for
![]() $\mathcal E_1(k), \mathcal E_2(k) $
, and
$\mathcal E_1(k), \mathcal E_2(k) $
, and
![]() $\mathcal E_3(k)$
in (3·19), we see that
$\mathcal E_3(k)$
in (3·19), we see that
The estimation of
![]() $S_2(k)$
is very similar and leads to the same bound. Hence, by (3·18)
$S_2(k)$
is very similar and leads to the same bound. Hence, by (3·18)
Inserting this into (3·16), we find that
 \begin{equation}\notag \begin{split} \sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) F_{\Omega}(\Re P({\gamma })-A) \ll_\ell X^{4CK\log\log X} \log T\int_0^\Omega G\Big(\frac \omega \Omega\Big) \sum_{1\leq k < K} \frac{(2\pi\omega )^k}{k!} \frac{\mathop{d\omega}}{\omega} +T. \end{split} \end{equation}
\begin{equation}\notag \begin{split} \sum_{0 < {\gamma } \leq T} e(\ell {\gamma }) F_{\Omega}(\Re P({\gamma })-A) \ll_\ell X^{4CK\log\log X} \log T\int_0^\Omega G\Big(\frac \omega \Omega\Big) \sum_{1\leq k < K} \frac{(2\pi\omega )^k}{k!} \frac{\mathop{d\omega}}{\omega} +T. \end{split} \end{equation}
As G is bounded over [0, 1], this is
By the choice of parameters
![]() $X, \Omega,$
and K in (3·7) and (3·11), it follows that for a fixed
$X, \Omega,$
and K in (3·7) and (3·11), it follows that for a fixed
![]() $\ell$
,
$\ell$
,
This establishes (3·9), and the same estimate clearly holds when A is replaced by B. This completes the proof that
![]() ${\Gamma }_{[a, b]}$
is uniformly distributed modulo one.
${\Gamma }_{[a, b]}$
is uniformly distributed modulo one.
Since the number of
![]() ${\gamma }$
’s in
${\gamma }$
’s in
![]() ${\Gamma }_{[a, b]}$
with
${\Gamma }_{[a, b]}$
with
![]() $0<{\gamma }\leq T$
that are not elements of
$0<{\gamma }\leq T$
that are not elements of
![]() ${\Gamma }_{[a, b]}^*$
(in other words, that are not simple) is at most o(N(T)), we see that
${\Gamma }_{[a, b]}^*$
(in other words, that are not simple) is at most o(N(T)), we see that
![]() ${\Gamma }_{[a, b]}^*$
is also uniformly distributed modulo one.
${\Gamma }_{[a, b]}^*$
is also uniformly distributed modulo one.
4. Proof of Theorem 1·3
By the Erdös–Turán inequality (see [
Reference Montgomery6
, Chapter 1, Corollary 1·1]), if L is a positive integer and
![]() $[\alpha,\beta]$
is a subinterval of [0,1], then
$[\alpha,\beta]$
is a subinterval of [0,1], then
 \begin{equation}\left| \sum_{\substack{0<{\gamma } \leq T, \\ \{ {\gamma } (\!\log T)/2\pi \} \in [\alpha,\beta]}} 1 \ \ - \ (\beta-\alpha)N(T) \right| \ \leq \ \frac{N(T) }{L+1} \ + \ 3\sum_{\ell\leq L} \frac{1}{\ell}\Bigg| \sum_{0<{\gamma }\leq T } e\Big(\ell {\gamma } \frac{\log T}{2\pi}\Big)\Bigg|.\end{equation}
\begin{equation}\left| \sum_{\substack{0<{\gamma } \leq T, \\ \{ {\gamma } (\!\log T)/2\pi \} \in [\alpha,\beta]}} 1 \ \ - \ (\beta-\alpha)N(T) \right| \ \leq \ \frac{N(T) }{L+1} \ + \ 3\sum_{\ell\leq L} \frac{1}{\ell}\Bigg| \sum_{0<{\gamma }\leq T } e\Big(\ell {\gamma } \frac{\log T}{2\pi}\Big)\Bigg|.\end{equation}
By Conjecture 1, for each integer
![]() $\ell >0$
,
$\ell >0$
,
 \begin{equation}\notag \sum_{0<{\gamma }\leq T } e\Big(\ell {\gamma } \frac{\log T}{2\pi}\Big)= \sum_{0 < {\gamma } \leq T} T^{i\ell \gamma} \ll T^{\frac12+\epsilon \ell}.\end{equation}
\begin{equation}\notag \sum_{0<{\gamma }\leq T } e\Big(\ell {\gamma } \frac{\log T}{2\pi}\Big)= \sum_{0 < {\gamma } \leq T} T^{i\ell \gamma} \ll T^{\frac12+\epsilon \ell}.\end{equation}
Hence, the right-hand side of (4·1) is
Taking
![]() $ \displaystyle L=[{1}/{2\epsilon}]$
and assuming that
$ \displaystyle L=[{1}/{2\epsilon}]$
and assuming that
![]() $0<\epsilon <1/2$
, we see that this is
$0<\epsilon <1/2$
, we see that this is
![]() $\ll \epsilon N(T)$
. Since
$\ll \epsilon N(T)$
. Since
![]() $\epsilon$
can be arbitrarily small, this establishes (1·5).
$\epsilon$
can be arbitrarily small, this establishes (1·5).
5. Proof of Theorem 1·4
By the Erdös–Turán inequality again, if L is a positive integer and
![]() $[\alpha,\beta]$
is a subinterval of [0,1], then
$[\alpha,\beta]$
is a subinterval of [0,1], then
 \begin{equation}\begin{split} & \left| \sum_{\substack{0<{\gamma } \leq T, {\gamma }\in {\Gamma }_{[a, b]}\\ \{ {\gamma } (\!\log T)/2\pi \} \in [\alpha,\beta]}} 1 \ \ - \ (\beta-\alpha)N_{[a, b]}(T) \right| \ \\& \qquad\qquad\qquad \leq \frac{N_{[a, b]}(T) }{L+1} \ + \ 3\sum_{\ell\leq L} \frac{1}{\ell}\Bigg| \sum_{0<{\gamma }\leq T, {\gamma }\in {\Gamma }_{[a, b]}} e\Big(\ell {\gamma } \frac{\log T}{2\pi}\Big)\Bigg|.\end{split}\end{equation}
\begin{equation}\begin{split} & \left| \sum_{\substack{0<{\gamma } \leq T, {\gamma }\in {\Gamma }_{[a, b]}\\ \{ {\gamma } (\!\log T)/2\pi \} \in [\alpha,\beta]}} 1 \ \ - \ (\beta-\alpha)N_{[a, b]}(T) \right| \ \\& \qquad\qquad\qquad \leq \frac{N_{[a, b]}(T) }{L+1} \ + \ 3\sum_{\ell\leq L} \frac{1}{\ell}\Bigg| \sum_{0<{\gamma }\leq T, {\gamma }\in {\Gamma }_{[a, b]}} e\Big(\ell {\gamma } \frac{\log T}{2\pi}\Big)\Bigg|.\end{split}\end{equation}
Thus, to prove (1·6), we need to estimate
 \begin{equation} \begin{split} \sum_{0<{\gamma }\leq T, {\gamma }\in {\Gamma }_{[a, b]}} e\Big(\ell {\gamma } \frac{\log T}{2\pi}\Big)=& \sum_{0 < {\gamma } \leq T} T^{i\ell {\gamma } } \,\, \unicode{x1D7D9}_{[a,b]}\Bigg(\frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log {\gamma })^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log {\gamma }}}\Bigg)\end{split} \end{equation}
\begin{equation} \begin{split} \sum_{0<{\gamma }\leq T, {\gamma }\in {\Gamma }_{[a, b]}} e\Big(\ell {\gamma } \frac{\log T}{2\pi}\Big)=& \sum_{0 < {\gamma } \leq T} T^{i\ell {\gamma } } \,\, \unicode{x1D7D9}_{[a,b]}\Bigg(\frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log {\gamma })^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log {\gamma }}}\Bigg)\end{split} \end{equation}
for positive integers
![]() $\ell$
. We do this, for the most part, by following the procedure of estimating the corresponding sum in (3·1) in the previous section. To start with, the same analysis that led to (3·2) leads to
$\ell$
. We do this, for the most part, by following the procedure of estimating the corresponding sum in (3·1) in the previous section. To start with, the same analysis that led to (3·2) leads to
 \begin{equation} \begin{split} & \sum_{0 < {\gamma } \leq T} T^{i\ell {\gamma } } \,\, \unicode{x1D7D9}_{[a,b]}\Bigg(\frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log {\gamma })^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log {\gamma }}}\Bigg)\\=&\sum_{0<{\gamma } \leq T} T^{i\ell {\gamma } } \,\, \unicode{x1D7D9}_{[a,b]} \Bigg(\frac{\Re P({\gamma })}{\sqrt{\frac12\log\log T}}\Bigg)+ O \bigg(N(T) \frac{(\!\log\log\log T)^2}{\sqrt{\log\log T}} \bigg).\end{split} \end{equation}
\begin{equation} \begin{split} & \sum_{0 < {\gamma } \leq T} T^{i\ell {\gamma } } \,\, \unicode{x1D7D9}_{[a,b]}\Bigg(\frac{\log \big(\big|\zeta^{(m_{\gamma })}(\frac12+i{\gamma }) \big|/(\!\log {\gamma })^{m_{\gamma }} \big) }{\sqrt{\frac12\log\log {\gamma }}}\Bigg)\\=&\sum_{0<{\gamma } \leq T} T^{i\ell {\gamma } } \,\, \unicode{x1D7D9}_{[a,b]} \Bigg(\frac{\Re P({\gamma })}{\sqrt{\frac12\log\log T}}\Bigg)+ O \bigg(N(T) \frac{(\!\log\log\log T)^2}{\sqrt{\log\log T}} \bigg).\end{split} \end{equation}
Similarly, the analysis that led to (3·8), with the same choices of the parameters A, B, X, and
![]() $\Omega$
, and Dirichlet polynomial P, shows that
$\Omega$
, and Dirichlet polynomial P, shows that
 \begin{equation}\begin{split}\sum_{0<{\gamma } \leq T}&T^{i\ell {\gamma } } \unicode{x1D7D9}_{[A, B]} ( \Re {P}({\gamma })) \\ = &\frac{1}{2} \sum_{0<{\gamma } \leq T} T^{i\ell {\gamma } } F_{\Omega} (\Re{ P({\gamma })}-A)-\frac{1}{2} \sum_{0<{\gamma } \leq T} T^{i\ell {\gamma } } F_{\Omega}(\Re {P}({\gamma })-B)+O\Big( \frac{N(T)}{\Omega}\Big) .\end{split}\end{equation}
\begin{equation}\begin{split}\sum_{0<{\gamma } \leq T}&T^{i\ell {\gamma } } \unicode{x1D7D9}_{[A, B]} ( \Re {P}({\gamma })) \\ = &\frac{1}{2} \sum_{0<{\gamma } \leq T} T^{i\ell {\gamma } } F_{\Omega} (\Re{ P({\gamma })}-A)-\frac{1}{2} \sum_{0<{\gamma } \leq T} T^{i\ell {\gamma } } F_{\Omega}(\Re {P}({\gamma })-B)+O\Big( \frac{N(T)}{\Omega}\Big) .\end{split}\end{equation}
And, similarly to (3·12), we find that
 \begin{align} \notag \sum_{0 < {\gamma } \leq T} T^{i\ell {\gamma } } F_{\Omega}(\Re {P}({\gamma })-A) = &\, F_\Omega(A) \sum_{0 < {\gamma } \leq T} T^{i\ell {\gamma } } \\ +\sum_{0 < {\gamma } \leq T} T^{i\ell {\gamma } } \Im \int_0^\Omega & G\Big(\frac \omega \Omega\Big) e^{-2\pi i A \omega} \sum_{1\leq k < K}\frac{(2\pi i\omega)^k}{k!} (\Re {P}({\gamma }))^k \frac{\mathop{d\omega}}{\omega}\\ \notag &+ O\bigg( \sum_{0 < {\gamma } \leq T} |\Re {P}({\gamma })|^K \int_0^\Omega G\Big(\frac \omega \Omega\Big) \frac{(2\pi\omega)^K}{K!} \frac{\mathop{d\omega}}{\omega} \bigg), \end{align}
\begin{align} \notag \sum_{0 < {\gamma } \leq T} T^{i\ell {\gamma } } F_{\Omega}(\Re {P}({\gamma })-A) = &\, F_\Omega(A) \sum_{0 < {\gamma } \leq T} T^{i\ell {\gamma } } \\ +\sum_{0 < {\gamma } \leq T} T^{i\ell {\gamma } } \Im \int_0^\Omega & G\Big(\frac \omega \Omega\Big) e^{-2\pi i A \omega} \sum_{1\leq k < K}\frac{(2\pi i\omega)^k}{k!} (\Re {P}({\gamma }))^k \frac{\mathop{d\omega}}{\omega}\\ \notag &+ O\bigg( \sum_{0 < {\gamma } \leq T} |\Re {P}({\gamma })|^K \int_0^\Omega G\Big(\frac \omega \Omega\Big) \frac{(2\pi\omega)^K}{K!} \frac{\mathop{d\omega}}{\omega} \bigg), \end{align}
where
![]() $K=2\big[(\!\log\log T)^6\big]$
.
$K=2\big[(\!\log\log T)^6\big]$
.
By (3·5),
![]() $F_{\Omega}(A) \ll 1$
and, by Conjecture 1,
$F_{\Omega}(A) \ll 1$
and, by Conjecture 1,
for any
![]() $\epsilon>0$
. Thus, the first term on the right-hand side of (5·5) is
$\epsilon>0$
. Thus, the first term on the right-hand side of (5·5) is
![]() $O(T^{\frac12+\epsilon \ell})$
. The third term is estimated in the same way as the third term in (3·12) and is likewise O(T). Hence
$O(T^{\frac12+\epsilon \ell})$
. The third term is estimated in the same way as the third term in (3·12) and is likewise O(T). Hence
 \begin{equation} \begin{split} & \sum_{0 < {\gamma } \leq T} T^{i\ell\gamma} F_{\Omega}(\Re{P}({\gamma })-A) \\ = &\int_0^\Omega G\Big(\frac \omega \Omega\Big) \sum_{1\leq k < K} \Im{\big(e^{-2\pi i A \omega}\, i^k\big)} \frac{(2\pi\omega)^k}{k!} \sum_{0 < {\gamma } \leq T} T^{i\ell\gamma} (\Re{P}({\gamma }))^k \frac{\mathop{d\omega}}{\omega} +O(T)+O(T^{\frac12+\epsilon \ell}). \end{split} \end{equation}
\begin{equation} \begin{split} & \sum_{0 < {\gamma } \leq T} T^{i\ell\gamma} F_{\Omega}(\Re{P}({\gamma })-A) \\ = &\int_0^\Omega G\Big(\frac \omega \Omega\Big) \sum_{1\leq k < K} \Im{\big(e^{-2\pi i A \omega}\, i^k\big)} \frac{(2\pi\omega)^k}{k!} \sum_{0 < {\gamma } \leq T} T^{i\ell\gamma} (\Re{P}({\gamma }))^k \frac{\mathop{d\omega}}{\omega} +O(T)+O(T^{\frac12+\epsilon \ell}). \end{split} \end{equation}
The remaining term here is handled in the same way as the corresponding term in (3·16), except that we use Conjecture 1 rather than Lemma 3·1 to estimate the sums over
![]() ${\gamma }$
. We carry this out now.
${\gamma }$
. We carry this out now.
Similarly to the analysis of the sum S(k) in (3·17) that gave (3·18), we find that
 \begin{equation}\notag \begin{split} \sum_{0 < {\gamma } \leq T} T^{i\ell\gamma} (\Re{P}({\gamma }))^k =&\frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_{0 < {\gamma } \leq T} T^{i\ell\gamma} \sum_n \frac{a_j(n)}{n^{1/2+i{\gamma }}} \sum_m \frac{a_{k-j}(m)}{m^{1/2-i{\gamma }}} \\ =&\frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{\sqrt n} \sum_m \frac{a_{k-j}(m)}{\sqrt m} \sum_{0 < {\gamma } \leq T} \Big(\frac{m T^\ell}{n}\Big)^{i{\gamma }}, \end{split} \end{equation}
\begin{equation}\notag \begin{split} \sum_{0 < {\gamma } \leq T} T^{i\ell\gamma} (\Re{P}({\gamma }))^k =&\frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_{0 < {\gamma } \leq T} T^{i\ell\gamma} \sum_n \frac{a_j(n)}{n^{1/2+i{\gamma }}} \sum_m \frac{a_{k-j}(m)}{m^{1/2-i{\gamma }}} \\ =&\frac{1}{2^k}\sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{\sqrt n} \sum_m \frac{a_{k-j}(m)}{\sqrt m} \sum_{0 < {\gamma } \leq T} \Big(\frac{m T^\ell}{n}\Big)^{i{\gamma }}, \end{split} \end{equation}
where, as before,
![]() $a_{r}(p_1\dots p_{r})$
denotes the number of permutations of the primes
$a_{r}(p_1\dots p_{r})$
denotes the number of permutations of the primes
![]() $p_1,\dots, p_{r}$
, which might or might not be distinct. By Conjecture 1, for each m and n
$p_1,\dots, p_{r}$
, which might or might not be distinct. By Conjecture 1, for each m and n
 \begin{equation*}\sum_{0 < {\gamma } \leq T} \Big(\frac{m T^\ell}{n}\Big)^{i{\gamma }}\ll T^{1+\ell \epsilon-\ell/2} \Big(\frac{m}{n}\Big)^{-\frac12+\epsilon}+T^{\frac12+\ell \epsilon} \Big(\frac{m}{n}\Big)^{\epsilon}.\end{equation*}
\begin{equation*}\sum_{0 < {\gamma } \leq T} \Big(\frac{m T^\ell}{n}\Big)^{i{\gamma }}\ll T^{1+\ell \epsilon-\ell/2} \Big(\frac{m}{n}\Big)^{-\frac12+\epsilon}+T^{\frac12+\ell \epsilon} \Big(\frac{m}{n}\Big)^{\epsilon}.\end{equation*}
Thus
 \begin{equation} \begin{split} & \sum_{0 < {\gamma } \leq T} T^{i\ell\gamma} (\Re{P}({\gamma }))^k \\ \ll \, & \frac{T^{1+\ell \epsilon-\frac{\ell}{2}}}{2^k} \sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{n^{\epsilon}} \sum_m \frac{a_{k-j}(m)}{m^{1-\epsilon}} + \frac{T^{\frac12+\ell \epsilon} }{2^k} \sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{n^{1/2+\epsilon}} \sum_m \frac{a_{k-j}(m)}{m^{1/2-\epsilon}}\\ &= \mathcal T_1(k)+ \mathcal T_2(k),\end{split}\end{equation}
\begin{equation} \begin{split} & \sum_{0 < {\gamma } \leq T} T^{i\ell\gamma} (\Re{P}({\gamma }))^k \\ \ll \, & \frac{T^{1+\ell \epsilon-\frac{\ell}{2}}}{2^k} \sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{n^{\epsilon}} \sum_m \frac{a_{k-j}(m)}{m^{1-\epsilon}} + \frac{T^{\frac12+\ell \epsilon} }{2^k} \sum_{j=0}^k \binom{k}{j} \sum_n \frac{a_j(n)}{n^{1/2+\epsilon}} \sum_m \frac{a_{k-j}(m)}{m^{1/2-\epsilon}}\\ &= \mathcal T_1(k)+ \mathcal T_2(k),\end{split}\end{equation}
say. Now
 \begin{equation} \notag \begin{split}\mathcal T_1(k)&\ll \frac{T^{1+\ell \epsilon-\frac{\ell}{2}}}{2^k} \sum_{j=0}^k \binom{k}{j} \sum_n {a_j(n)} \sum_m {a_{k-j}(m)} \\& \ll \frac{T^{1+\ell \epsilon-\frac{\ell}{2}}}{2^k}\sum_{j=0}^k \binom{k}{j} \Bigg( \sum_{p\leq X^2}1\Bigg)^j \Bigg( \sum_{p\leq X^2} 1\Bigg)^{k-j} \ll T^{\frac12+\ell \epsilon }\pi(X^2)^k, \end{split} \end{equation}
\begin{equation} \notag \begin{split}\mathcal T_1(k)&\ll \frac{T^{1+\ell \epsilon-\frac{\ell}{2}}}{2^k} \sum_{j=0}^k \binom{k}{j} \sum_n {a_j(n)} \sum_m {a_{k-j}(m)} \\& \ll \frac{T^{1+\ell \epsilon-\frac{\ell}{2}}}{2^k}\sum_{j=0}^k \binom{k}{j} \Bigg( \sum_{p\leq X^2}1\Bigg)^j \Bigg( \sum_{p\leq X^2} 1\Bigg)^{k-j} \ll T^{\frac12+\ell \epsilon }\pi(X^2)^k, \end{split} \end{equation}
since
![]() $\ell \geq 1$
. Similarly,
$\ell \geq 1$
. Similarly,
 \begin{equation} \notag \begin{split}\mathcal T_2(k)&\ll \frac{T^{\frac12+\ell \epsilon} }{2^k} \sum_{j=0}^k \binom{k}{j} \sum_n {a_j(n)} \sum_m {a_{k-j}(m)} = T^{\frac12+\ell \epsilon} \pi(X^2)^k. \end{split} \end{equation}
\begin{equation} \notag \begin{split}\mathcal T_2(k)&\ll \frac{T^{\frac12+\ell \epsilon} }{2^k} \sum_{j=0}^k \binom{k}{j} \sum_n {a_j(n)} \sum_m {a_{k-j}(m)} = T^{\frac12+\ell \epsilon} \pi(X^2)^k. \end{split} \end{equation}
Combining our estimates for
![]() $\mathcal T_1(k)$
and
$\mathcal T_1(k)$
and
![]() $\mathcal T_2(k)$
in (5·7), we see that
$\mathcal T_2(k)$
in (5·7), we see that
Using this in (5·6), we find that
 \begin{equation} \notag \begin{split} \sum_{0 < {\gamma } \leq T} T^{i\ell\gamma} F_{\Omega}(\Re{P}({\gamma })-A) &\ll T^{\frac12+\ell \epsilon} \ X^{2K} \! \int_0^\Omega\! G\Big(\frac \omega \Omega\Big) \sum_{1\leq k < K} \frac{(2\pi\omega)^k}{k!} \frac{\mathop{d\omega}}{\omega} + O(T) +O(T^{\frac12+\epsilon \ell})\\ &\ll \Omega e^{2\pi \Omega} \ T^{\frac12+\ell \epsilon} \ X^{2K} + O(T) .\end{split}\end{equation}
\begin{equation} \notag \begin{split} \sum_{0 < {\gamma } \leq T} T^{i\ell\gamma} F_{\Omega}(\Re{P}({\gamma })-A) &\ll T^{\frac12+\ell \epsilon} \ X^{2K} \! \int_0^\Omega\! G\Big(\frac \omega \Omega\Big) \sum_{1\leq k < K} \frac{(2\pi\omega)^k}{k!} \frac{\mathop{d\omega}}{\omega} + O(T) +O(T^{\frac12+\epsilon \ell})\\ &\ll \Omega e^{2\pi \Omega} \ T^{\frac12+\ell \epsilon} \ X^{2K} + O(T) .\end{split}\end{equation}
provided
![]() $\ell\leq L$
and
$\ell\leq L$
and
![]() $\epsilon$
is small enough relative to L. Inserting this (and the same estimate when A is replaced by B) into (5·4), we find that
$\epsilon$
is small enough relative to L. Inserting this (and the same estimate when A is replaced by B) into (5·4), we find that
By (5·2) and (5·3) we then obtain
 \begin{equation}\notag \sum_{0<{\gamma }\leq T, {\gamma }\in {\Gamma }_{[a, b]}} e\Big(\ell {\gamma } \frac{\log T}{2\pi}\Big) \ll N(T) \frac{(\!\log\log\log T)^2}{\sqrt{\log\log T}}\end{equation}
\begin{equation}\notag \sum_{0<{\gamma }\leq T, {\gamma }\in {\Gamma }_{[a, b]}} e\Big(\ell {\gamma } \frac{\log T}{2\pi}\Big) \ll N(T) \frac{(\!\log\log\log T)^2}{\sqrt{\log\log T}}\end{equation}
for
![]() $\ell\leq L$
. Using this bound in (5·1), we see that
$\ell\leq L$
. Using this bound in (5·1), we see that
 \begin{equation}\notag \left| \sum_{\substack{0<{\gamma } \leq T, {\gamma }\in {\Gamma }_{[a, b]}\\ \{ {\gamma } (\!\log T)/2\pi \} \in [\alpha,\beta]}} 1 \ \ - \ (\beta-\alpha)N_{[a, b]}(T) \right|\ \ll \ \frac{N_{[a, b]}(T) }{L+1} \ + \ N(T) (\!\log L) \frac{(\!\log\log\log T)^2}{\sqrt{\log\log T}}.\end{equation}
\begin{equation}\notag \left| \sum_{\substack{0<{\gamma } \leq T, {\gamma }\in {\Gamma }_{[a, b]}\\ \{ {\gamma } (\!\log T)/2\pi \} \in [\alpha,\beta]}} 1 \ \ - \ (\beta-\alpha)N_{[a, b]}(T) \right|\ \ll \ \frac{N_{[a, b]}(T) }{L+1} \ + \ N(T) (\!\log L) \frac{(\!\log\log\log T)^2}{\sqrt{\log\log T}}.\end{equation}
By our hypotheses on a and b,
![]() $N_{[a,b]}(T)\gg N(T)$
. Hence, since L may be arbitrarily large, we find that this equals
$N_{[a,b]}(T)\gg N(T)$
. Hence, since L may be arbitrarily large, we find that this equals
![]() $o(N_{[a, b]}(T))$
. This proves (1·6). The analogous inequality when
$o(N_{[a, b]}(T))$
. This proves (1·6). The analogous inequality when
![]() ${\Gamma }_{[a, b]}$
is replaced by
${\Gamma }_{[a, b]}$
is replaced by
![]() ${\Gamma }_{[a, b]}^*$
follows from this on noting that the number of
${\Gamma }_{[a, b]}^*$
follows from this on noting that the number of
![]() ${\gamma }$
in
${\gamma }$
in
![]() ${\Gamma }_{[a, b]}$
with
${\Gamma }_{[a, b]}$
with
![]() $0<{\gamma }\leq T$
that are not elements of
$0<{\gamma }\leq T$
that are not elements of
![]() ${\Gamma }_{[a, b]}^*$
is at most
${\Gamma }_{[a, b]}^*$
is at most
![]() $o(N_{[a,b]}(T))$
.
$o(N_{[a,b]}(T))$
.
Acknowledgements
We thank the anonymous referee for their careful reading of our paper and for pointing out an error in the original version. The first author thanks the Indian Institute of Technology Gandhinagar, where this work was begun, for its hospitality. She is also grateful for a postdoctoral fellowship from the Pacific Institute for the Mathematical Sciences at the University of Northern British Columbia, where this work was completed.