Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-30T20:45:42.578Z Has data issue: false hasContentIssue false
  • English
  • Français

Über die monotone Konvergenz der Cesàro-Mittel bei Fourier- und Potenzreihen

Published online by Cambridge University Press:  24 October 2008

P. Turán
P. Turán
Affiliation:
Budapest
Get access Rights & Permissions [Opens in a new window]

Extract

1·1. Es bezeichne für nichtnegative ganze n und k

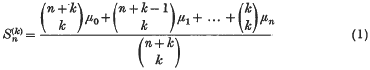
das n-te Cesàro-Mittel der Ordnung k der Reihe μ0 + μ1 + … Insbesondere ist also 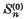die n-te Partialsumme dieser Reihe.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 34 , Issue 2 , April 1938 , pp. 134 - 143
Copyright
Copyright © Cambridge Philosophical Society 1938

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

† Fejér, L., Math. Annalen, 58 (1904), 51–69.CrossRefGoogle Scholar

‡ Eine Vereinfachung im Beweise verdanke ich einer freundlichen Mitteilung von Herrn Prof. W. Rogosinski.

† Für nichtganze k sind in (1) die Grössen durch zu ersetzen.

‡ Vergl. Fejér, L., Rendiconti di Palermo, 38 (1914), 79–97.CrossRefGoogle Scholar

§ Der Satz ist für k = 1 allgemein nicht richtig.

† Es ist sin xdx ≥ 0.

‡ Koschmieder, L., Monatsh. f. Math. u. Phys. 39 (1932), 321–41.CrossRefGoogle Scholar

§ Fejér, L., Zeit. f. angew. Math. u. Mech. 13 (1933), 80–8.CrossRefGoogle Scholar

∥ Turán, P., Journal London Math. Soc. 10 (1935), 277–80.CrossRefGoogle Scholar

† Es ist

‡ Fejér, L., Proc. Cambridge Phil. Soc. 31 (1935), 307–16.CrossRefGoogle Scholar

§ Szegö, L. Fejér u. G., Prace Matematyczno Fizyczne, 44 (1937), 1–11.Google Scholar

† Nach Voraussetzung ist C endlich.

† Zuerst im Falle λk = 1/k 2 bewiesen bei Koschmieder loc. cit.; allgemein, mit der Bedingung λk≥ 0, steht das Lemma bei Fejér, Journal of Math. and Physics, 13 (1934), 1.Google ScholarDen hier gegebenen Beweis hatte uns Herr Prof. Fejér zur Verfügung gestellt.

† Scheinbar ist statt f(x) ≥ 0 nur f(O) ≥ 0 benutzt. Das erstere ist aber eine Folge hiervon wegen der Konvexität und Symmetrie.

† bedeutet die zu b konjugiert komplexe Zahl.

† Leere Summen (im Falle n = 0) bedeuten 0.

‡ Für cos π = 0 ist