Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T14:28:15.268Z Has data issue: false hasContentIssue false
  • English
  • Français

Two notes on the Riemann Zeta-function*

Published online by Cambridge University Press:  24 October 2008

J. E. Little-wood
J. E. Little-wood
Affiliation:
Trinity College, Cayley Lecturer
Get access Rights & Permissions [Opens in a new window]

Extract

Let Λ (n) be the arithmetic function usually so denoted, which is zero unless n is a prime power pm (m ≥ 1), when it is log p. We write as usual

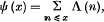
and

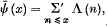
where the dash denotes that if x is an integer the last term Λ (x) of the sum is to be taken with a factor ½. We wrute further

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 22 , Issue 3 , 20 September 1924 , pp. 234 - 242
Copyright
Copyright © Cambridge Philosophical Society 1924

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

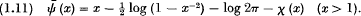
† Landau, E., “Über einige Summen, die von den Nullstellen der Riemannschen Zetafunktion abhängen,” Acta Math., 35 (1911), pp. 271–294.CrossRefGoogle Scholar

‡ Our convention as to the use of O implies, of course, that the formula holds “uniformly for y ≥ √x.”

* I hope to publish this result shortly in another paper.

* Since all roots with γ > 0 lie in 0 < σ < 1, and are symmetrically disposed about the line σ = frac12;

† s 0 is a pure imaginary, and s describes the real axis as ζ describes the large rectangle.

* Here and in the argument below we use the inequality

A glance at the inequalities immediately following verifies the condition |z| < ½.

* Γ4 extends to the left (only) as far as σ = − 19.

† We naturally choose the determination of log ζ defined by the Dirichlet series for σ > 1.