Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-30T21:37:54.034Z Has data issue: false hasContentIssue false
  • English
  • Français

Transposable character tables and group duality

Published online by Cambridge University Press:  28 April 2014

IVAN ANDRUS ,
PÁL HEGEDŰS  and
TETSURO OKUYAMA
IVAN ANDRUS
Affiliation:
Department of Mathematics and its Applications, Central European UniversityNador utca 9, 1051 Budapest, Hungary. e-mail: [email protected], [email protected]
PÁL HEGEDŰS
Affiliation:
Department of Mathematics and its Applications, Central European UniversityNador utca 9, 1051 Budapest, Hungary. e-mail: [email protected], [email protected]
TETSURO OKUYAMA
Affiliation:
Laboratory of Mathematics, Hokkaido University of Education, Asahikawa, Hokkaido 070-0825, Japan. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

One way of expressing the self-duality 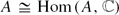$A\cong {\rm Hom}(A,\mathbb{C})$ of Abelian groups is that their character tables are self-transpose (in a suitable ordering). In this paper we extend the duality to some noncommutative groups considering when the character table of a finite group is close to being the transpose of the character table for some other group. We find that groups dual to each other have dual normal subgroup lattices. We show that our concept of duality cannot work for non-nilpotent groups and we describe p-group examples.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 157 , Issue 1 , July 2014 , pp. 31 - 44
Copyright
Copyright © Cambridge Philosophical Society 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Andrus, Ivan Transposable character tables. PhD. thesis. Central European University (2013).Google Scholar
[2]Bannai, EiichiAssociation schemes and fusion algebras (an introduction). J. Algebraic Combin. 2 (1993), 327–344.CrossRefGoogle Scholar
[3]Bianchi, Mariagrazia, Chillag, David, Lewis, Mark L. and Pacifici, EmanueleCharacter degree graphs that are complete graphs. Proc. Amer. Math. Soc. 135 (2007), 671–676 (electronic).CrossRefGoogle Scholar
[4]Camina, Alan R. and Camina, Rachel D.The influence of conjugacy class sizes on the structure of finite groups: a survey. Asian–Eur. J. Math. 4 (2011), 559–588.CrossRefGoogle Scholar
[5]Fisman, Elsa and Arad, ZviA proof of Szep's conjecture on nonsimplicity of certain finite groups. J. Algebra. 108 (1987), 340–354.CrossRefGoogle Scholar
[6]The GAP Group GAP – Groups, Algorithms and Programming, Version 4.4.12, (2008).Google Scholar
[7]Hanaki, Akihide Self dual groups and finite symmetric algebras self dual groups and finite symmetric algebras of Loewy length 4. http://math.shinshu-u.ac.jp/~hanaki/notes.html (1996).Google Scholar
[8]Hanaki, AkihideSelf-dual groups of order p 5 (p an odd prime). Osaka J. Math. 34 (1997), 357–361.Google Scholar
[9]Hanaki, Akihide and Okuyama, TetsuroGroups with some combinatorial properties. Osaka J. Math. 34 (1997), 337–356.Google Scholar
[10]Isaacs, Irving M. and Smith, Stephen D.A note on groups of p-length 1. J. Algebra. 38 (1976), 531–535.CrossRefGoogle Scholar
[11]Isaacs, Irving M.Character Theory of Finite Groups. (Academic Press, New York, 1976).Google Scholar
[12]James, RodneyThe groups of order p 6 (p an odd prime). Math. Comp. 34 (1980), 613–637.Google Scholar
[13]Lewis, Mark L.An overview of graphs associated with character degrees and conjugacy class sizes in finite groups. Rocky Mountain J. Math. 38 (2008), 175–211.CrossRefGoogle Scholar
[14]Riedl, Jeffrey M.Character degrees, class sizes and normal subgroups of a certain class of p-groups. J. Algebra. 218 (1999), 190–215.CrossRefGoogle Scholar
[15]Sagirov, I. A.A generalization of the Suzuki 2-groups A(m,θ). Izv. Vyssh. Uchebn. Zaved. Mat. 10 (2003), 56–61.Google Scholar