Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-20T18:35:35.939Z Has data issue: false hasContentIssue false
  • English
  • Français

Topological properties of real simple germs, curves, and the nice dimensions n > p

Published online by Cambridge University Press:  24 October 2008

James Damon
James Damon
Affiliation:
University of North Carolina, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

Infinitesimally stable germs play an important role both as germs from which global C∞-stable mappings are constructed and as germs representing versal unfoldings of (C∞ or holomorphic) germs. Because of the presence of moduli, the C∞ (or analytic) classification of these germs is insufficient and the topological classification of these germs must be understood as well. Here we consider the classification of such germs in the region where no moduli occur. This region is important for several reasons. Most importantly, it contains the infinitesimally stable germs occurring in the nice dimensions. These are the dimensions in which globally infinitesimally stable mappings are dense among the proper C∞-mappings. In (4), it was proved that the topological and C∞-classifications agree for infinitesimally stable germs f: 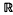n, 0 → 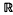p, 0 in the nice dimensions, n ≤ p. This was then used in (5) to characterize those topologically stable germs which are C∞-stable.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 89 , Issue 3 , May 1981 , pp. 457 - 472
Copyright
Copyright © Cambridge Philosophical Society 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Arnold, V. I.The normal forms of functions with simple critical points, the Weyl groups, Ak, Dk, Ek, and Lagrange manifolds. Functional Anal. Appl. 6, no. 4 (1972), 3–25.Google Scholar
(2)Brieskorn, E.Singular elements of semi-simple algebraic groups. Actes du Congrès Intern. des Math. 2 (1970), 279–284.Google Scholar
(3)Callahan, J.Singularities and plane maps. II. Sketching catastrophes. Amer. Math. Monthly 84 (1977), 765–803.CrossRefGoogle Scholar
(4)Damon, J.Topological properties of discrete algebra types. I. The Hilbert-Samuel Function. Adv. in Math. Supp Ser 5 (1978), 83–118. II. Real and complex algebras. Amer. Jour. Math. 101 (1979), 1219–1248.Google Scholar
(5)Damon, J.Topological stability in the nice dimensions, n < p. Bull Amer. Math. Soc. 86 (1976), pp. 262–264.CrossRefGoogle Scholar
(5)Damon, J.Topological stability in the nice dimensions, n < p. Topological stability in the nice dimensions. Topology 18 (1979), 129–142.Google Scholar
(6)Damon, J. and Galligo, A. The Hilbert-Samuel partition of Σ2. (Preprint.)Google Scholar
(7)Giusti, M.Classification des singularitiés isolées d'intersections complètes simples. C. R. Acad. Sc. Paris 284 (17/1/77).Google Scholar
(8)Looijenga, E.On the semi-universal deformation of a simple elliptic hypersurface singularity. I: Unimodularity. Topology 16 (1977), 257–262. II: The discriminant. Topology 17 (1978), 23–40.CrossRefGoogle Scholar
(9)Mather, J.Stability of C∞-mappings. III: Finitely determined map germs. Publ. I.H.E.S. 35 (1968), 127–156. IV: Classification of stable germs by R-algebras. Publ. I.H.E.S. 37 (1969), 237–248. VI: The nice dimensions. Liverpool Singularities Symposium. Springer Lecture Notes, no. 192 (1971), pp. 207–253.Google Scholar
(10)Mather, J. and Damon, J. Book on stability of mappings. (In preparation.)Google Scholar
(11)May, R. Transversality properties of topologically stable mappings, (Thesis, Harvard University 1973).Google Scholar
(12)Milnor, J.Singular points of complex hypersurfaces. Annals of Math. Studies 61 (1968).Google Scholar
(13)Pham, F. Remarque sur l'equisingularité universelle (University Nice, preprint, 1970).Google Scholar
(14)Siersma, D. Classification and deformation of singularities (Thesis, University of Amsterdam, 1974).Google Scholar