No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Classical bifurcation theorems for a 1 -parameter family of plane dynamical systems
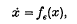
assert the presence of closed orbits clustering at some distinguished parameter value (∈ = 0, say). Here, for any ∈, the origin is the only stationary point. The topological content of the mostly analytic hypotheses imposed is some change in the stability behaviour of the origin at ∈ = 0, roughly the passing of a kind of stability to a kind of instability. Topologically speaking, e.g. some of the conditions demanded are asymptotic stability of the origin for the negative system 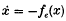 at ∈ > 0 and asymptotic stability of the origin for
at ∈ > 0 and asymptotic stability of the origin for 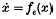 at ∈ < 0 (Hopf (8), Ruelle and Takens(11)) or ∈ = 0 (Chafee(2)).
at ∈ < 0 (Hopf (8), Ruelle and Takens(11)) or ∈ = 0 (Chafee(2)).