Castelnuovo has shown that the maximum freedom of a linear system of curves of genus p is 3p + 5, and that a system with this maximum freedom consists of hyperelliptic curves which can be transformed into a system of curves of order n with an (n − 2)-ple base point and a certain number of double base points; the only exceptions being that when p = 3 the system may be transformable into that of all quartics, and when p = 1 the system may be transformable into that of all cubics. Further, since, in the transformed system, the characteristic series is a 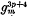it is non-special and hence the redundancy of the base points is zero, therefore each of the double points of this system reduces the freedom by exactly three; and hence if we remove all the double points we get a system of curves of genus p′ and freedom r′ = 3p′ + 5 with only one base point. If we take this point for origin the system of curves can be represented by a single Newton polygon containing in its interior exactly p points, collinear since the curves are hyperelliptic (p ≠ 3), and containing on its boundary 2p + 6 points. From this we can deduce immediately a theorem concerning convex polygons drawn on squared paper; I shall now give an a priori proof of this theorem.