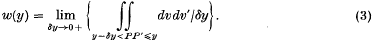Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-16T18:06:31.736Z Has data issue: false hasContentIssue false
  • English
  • Français

A theorem on multiple integrals

Published online by Cambridge University Press:  24 October 2008

J. M. Hammersley  and
P. A. P. Moran
J. M. Hammersley
Affiliation:
Lectureship in the design and analysis of scientific experimentUniversity of Oxford
Get access Rights & Permissions [Opens in a new window]

Extract

Suppose that dυ and dυ′ are two volume elements situated at points P and P′ respectively in a three-dimensional right circular cylinder, that y is the distance PP′, that z(y) is a given function of y, and that we wish to evaluate the sixfold integral

taken over all pairs of points P, P′ within the cylinder. We observe that z(y) is a function of y only; so that the sixfold integral can be expressed as a single integral

that is to say a weighted mean of z(y) over the relevant values of y, where the weight function is evidently given by

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 47 , Issue 2 , April 1951 , pp. 274 - 278
Copyright
Copyright © Cambridge Philosophical Society 1951

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Cramér, H.Mathematical methods of statistics (Princeton University Press, 1946).Google Scholar
(2)Ghosh, B.Topographic variation in statistical fields. Bull. Calcutta Statist. Ass. 2 (1949), 11–28.CrossRefGoogle Scholar
(3)Matérn, B.Metoder att uppskata noggrannhetten vid linje- och provytetaxering (Stockholm, 1947). Medd. från Statens Skogsforskningsinstitut, Band 36: 1.Google Scholar
(4)Saks, S.Theory of the integral. Monografie Matematyczne, Tom VII (Warsaw, 1937).Google Scholar
(5)von Neumann, J.Functional operators. Vol. I. Measures and integrals. Ann. Math. Studies, 21 (Princeton University Press, 1950).Google Scholar