Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T13:39:33.496Z Has data issue: false hasContentIssue false
  • English
  • Français

A theorem on bounded synthesis

Published online by Cambridge University Press:  24 October 2008

E. Galanis
E. Galanis
Affiliation:
Fitzwilliam College, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

Let G be a locally compact Abelian group.

DEFINITION 1. A compact subset K ⊂ G is called Kroneclcer set if for every continuous function f on K of modulus identically one (|f(x)| = 1, ∀x ∈ K) and for every ε 0 there exists x ∈ Ĝ such that

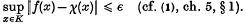
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 70 , Issue 1 , July 1971 , pp. 23 - 26
Copyright
Copyright © Cambridge Philosophical Society 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Rudin, W.Fourier analysis on groups. Interscience, Tracts n 12, 1962.Google Scholar
(2)Kahane, J.-P. and Salem, R.Ensembles parfaits et séries trigonométriques (Hermann, Paris, 1963).Google Scholar
(3)Kahane, J.-P.Séries de Fourier absolument convergentes (Springer, 1970)CrossRefGoogle Scholar
(4)Varopoulos, N. Th.Groups of continuous functions in harmonic analysis. Acta Math. 125 (1970), 109–154.CrossRefGoogle Scholar
(5)Varopoulos, N. Th.Sur les ensembles parfaits des séries trigonométriques. C. R. Acad. Sci., Paris 260, 3831–3834.Google Scholar
(6)Looms, L. H.The spectral characterization of a class of almost periodic functions. Ann. of Math. (2) 72 (1960), 362–368.CrossRefGoogle Scholar