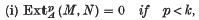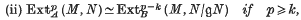Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Northcott, D. G.
1957.
A note on the global dimension of polynomial rings.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 53,
Issue. 4,
p.
796.
Rees, D.
1957.
The grade of an ideal or module.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 53,
Issue. 1,
p.
28.
Rees, D.
1957.
Polar modules.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 53,
Issue. 3,
p.
554.
Northcott, D. G.
1961.
Simple reduction theorems for extension and torsion functors.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 57,
Issue. 3,
p.
483.
Burch, Lindsay
1968.
A note on the homology of ideals ǵenerated by three elements in local rings.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 64,
Issue. 4,
p.
949.
Burch, Lindsay
1968.
On ideals of finite homoloǵical dimension in local rings.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 64,
Issue. 4,
p.
941.
Sharp, Rodney Y.
1969.
The cousin complex for a module over a commutative Noetherian ring.
Mathematische Zeitschrift,
Vol. 112,
Issue. 5,
p.
340.
Eisenreich, Günther
1971.
Beiträge zur Algebra und Geometrie 1.
p.
57.
Kaplansky, Irving
1973.
Conference on Commutative Algebra.
Vol. 311,
Issue. ,
p.
153.
Schochet, Claude
1979.
Acyclic ideals and Koszul complexes.
Journal of Pure and Applied Algebra,
Vol. 14,
Issue. 3,
p.
311.
Sharp, R. Y.
1981.
Cohen–Macaulay properties for balanced big Cohen–Macaulay modules.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 90,
Issue. 2,
p.
229.
Sharp, R. Y.
and
Zakeri, H.
1982.
Modules of generalized fractions.
Mathematika,
Vol. 29,
Issue. 1,
p.
32.
1984.
Analytic Sets in Locally Convex Spaces.
Vol. 89,
Issue. ,
p.
269.
Sharp, R. Y.
and
V�mos, P.
1985.
Baire's category theorem and prime avoidance in complete local rings.
Archiv der Mathematik,
Vol. 44,
Issue. 3,
p.
243.
Avramov, Luchezar L
and
Buchweitz, Ragnar-Olaf
2000.
Homological Algebra Modulo a Regular Sequence with Special Attention to Codimension Two.
Journal of Algebra,
Vol. 230,
Issue. 1,
p.
24.
Martin, Heath M.
2000.
Linkage and the generic homology of modules.
Communications in Algebra,
Vol. 28,
Issue. 9,
p.
4285.
Rump, Wolfgang
2003.
A Class of Auslander-Regular Macaulay Rings.
Communications in Algebra,
Vol. 31,
Issue. 12,
p.
6161.
Schneider, Peter
and
Venjakob, Otmar
2006.
On the codimension of modules over skew power series rings with applications to Iwasawa algebras.
Journal of Pure and Applied Algebra,
Vol. 204,
Issue. 2,
p.
349.
Hummel, Livia
2014.
Commutative Algebra.
p.
195.
Lawson, Mark V.
O’Carroll, Liam
and
Rees, Sarah
2014.
David Rees 1918–2013.
Semigroup Forum,
Vol. 88,
Issue. 3,
p.
513.