The Temperature Dependence of the Photo-Electric Effect
Published online by Cambridge University Press: 24 October 2008
Extract
The temperature dependence of the photo-electric effect with the image field is discussed, the result obtained agreeing with Fowler's T2 law near the threshold. Fowler's 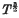 law is discussed, and shown to rest upon a mistake in the normalization of the free wave functions.
law is discussed, and shown to rest upon a mistake in the normalization of the free wave functions.
The two methods of analysing experimental results due to Fowler and Du Bridge are also discussed, and it is shown that in general the latter should give the more reliable results.
The author wishes to repeat his thanks to Prof. R. H. Fowler and to Mr A. H. Wilson for their constant interest in the work.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 31 , Issue 3 , July 1935 , pp. 416 - 428
- Copyright
- Copyright © Cambridge Philosophical Society 1935
References
page 416 note * Mitchell, K., Proc. Roy. Soc. A, 146 (1934), 442CrossRefGoogle Scholar; referred to as I throughout this paper.
page 416 note † Ig. Tamm, and Schubin, S., Zeits. Physik, 68 (1931), 97CrossRefGoogle Scholar; Fröhlich, H., Ann. Physik, 7 (1930), 103CrossRefGoogle Scholar; Wentzel, G., Sommerfeld Festschrift Probleme der Modernen Physik, edited by P., Debye, p. 79 (Hirzel, 1928).Google Scholar
page 416 note ‡ Fowler, R. H., Phys. Rev. 38 (1931), 45.CrossRefGoogle Scholar
page 416 note § Young, L. A. and Frank, N. H., Phys. Rev. 38 (1931), 838.CrossRefGoogle Scholar
page 416 note ∥ Blochinzew, D., Phys. Z. Sowjetunion, 1 (1931), 781.Google Scholar
page 417 note * Bridge, L. A. Du, Phys. Rev. 39 (1932), 108.Google Scholar
page 418 note * Whittaker and Watson, Modern Analysis, Chap. xvi. Further references to this will be given in the form WW.
page 424 note † Nordheim, L. W., Proc. Roy. Soc. A, 121 (1928), 626.CrossRefGoogle Scholar
page 425 note * This is not expressly stated in his paper, but he has made it clear in conversations with the author.
page 427 note * Compare the case of the simple potential discontinuity, discussed in I. Without giving the full result for this case, we may note that the final formula will contain a power of ν, as well as a complicated function of the optical constants.
page 427 note † Bridge, L. A. Du, Phys. Rev. 39 (1932), 108.Google Scholar
- 26
- Cited by


