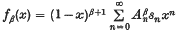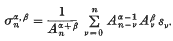Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kangro, G. F.
1976.
Theory of summability of sequences and series.
Journal of Soviet Mathematics,
Vol. 5,
Issue. 1,
p.
1.
Savaş, Ekrem
and
Şevli, Hamdullah
2007.
On extension of a result of Flett for Cesáro matrices.
Applied Mathematics Letters,
Vol. 20,
Issue. 4,
p.
476.
Savaş, E.
Şevli, H.
and
Rhoades, B. E.
2008.
On the Cesáro Summability of Double Series.
Journal of Inequalities and Applications,
Vol. 2008,
Issue. ,
p.
1.
Savaş, Ekrem
and
Rhoades, B. E.
2009.
Every conservative double Hausdorff matrix is a kth absolutely summable operator.
Analysis Mathematica,
Vol. 35,
Issue. 4,
p.
249.
Savaş, E.
Şevli, H.
and
Rhoades, B.E.
2009.
Sufficient Conditions for Factorable Matrices to be Bounded Operators on ${\cal A}_k$.
Rocky Mountain Journal of Mathematics,
Vol. 39,
Issue. 2,
Yu, Dansheng
2009.
On a result of Flett for Cesáro matrices.
Applied Mathematics Letters,
Vol. 22,
Issue. 12,
p.
1803.
Bor, Hüseyin
and
Yu, Dansheng
2011.
A new application of almost increasing and quasi-monotone sequences.
Applied Mathematics Letters,
Vol. 24,
Issue. 8,
p.
1347.
Bor, Hüseyin
2011.
A study on generalized quasi-power increasing sequences.
Russian Mathematics,
Vol. 55,
Issue. 6,
p.
15.
Bor, Hüseyin
2011.
An application of almost increasing sequences.
Applied Mathematics Letters,
Vol. 24,
Issue. 3,
p.
298.
Bor, Hüseyi̇n
2011.
Factors for generalized absolute Cesàro summability.
Mathematical and Computer Modelling,
Vol. 53,
Issue. 5-6,
p.
1150.
Bor, Hüseyin
2011.
On Generalized Absolute Cesàro Summability.
Annals of the Alexandru Ioan Cuza University - Mathematics,
Vol. 57,
Issue. 2,
p.
323.
Tuncer, A Nihal
2012.
On generalized absolute Cesàro summability factors.
Journal of Inequalities and Applications,
Vol. 2012,
Issue. 1,
Sarigöl, Mehmet Ali
2012.
Matrix operators on sequence Ak.
Mathematical and Computer Modelling,
Vol. 55,
Issue. 5-6,
p.
1763.
Yu, Dansheng
and
Zhou, Ping
2013.
A new class of matrices and its applications to absolute summability factor theorems.
Mathematical and Computer Modelling,
Vol. 57,
Issue. 3-4,
p.
401.
Sulaiman, W. T.
2013.
Some new factor theorem for absolute summability.
Demonstratio Mathematica,
Vol. 46,
Issue. 1,
p.
149.
Şevli, Hamdullah
and
Savaş, Rabia
2014.
On double Hausdorff summability method.
Journal of Inequalities and Applications,
Vol. 2014,
Issue. 1,
Bor, H.
2016.
A New Application of Quasimonotone Sequences.
Ukrainian Mathematical Journal,
Vol. 68,
Issue. 7,
p.
1146.
Bor, Hüseyin
2016.
A new application of non-increasing sequences.
Positivity,
Vol. 20,
Issue. 1,
p.
131.
Hazar, G. Canan
and
Sarigöl, M. Ali
2018.
On Absolute Nörlund Spaces and Matrix Operators.
Acta Mathematica Sinica, English Series,
Vol. 34,
Issue. 5,
p.
812.
Canan Hazar, G.
and
Ali Sarıgöl, M.
2018.
Absolute Cesàro Series Spaces and Matrix Operators.
Acta Applicandae Mathematicae,
Vol. 154,
Issue. 1,
p.
153.
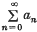 be the given infinite series with {sn} as the sequence of partial sums and let
be the given infinite series with {sn} as the sequence of partial sums and let 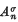 be the binomial coefficient of zn in the power series expansion of the function (l-z)-σ-1 |z| < 1. Now let, for β > – 1,
be the binomial coefficient of zn in the power series expansion of the function (l-z)-σ-1 |z| < 1. Now let, for β > – 1,