Symmetric energy-momentum tensors in relativistic field theories
Published online by Cambridge University Press: 24 October 2008
Extract
In relativistic field theories derived by a variation principle from a Lagrangian, the problem arises of finding a symmetric tensor of rank 2 which has vanishing divergence in virtue of the field equations and is such that 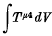 taken over a space-like section is equal to the corresponding integral of the so-called canonical energy-momentum tensor. It is well known that the latter condition is satisfied if the difference between the two tensors is the divergence of an antisymmetric tensor of rank 3.
taken over a space-like section is equal to the corresponding integral of the so-called canonical energy-momentum tensor. It is well known that the latter condition is satisfied if the difference between the two tensors is the divergence of an antisymmetric tensor of rank 3.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 43 , Issue 4 , October 1947 , pp. 511 - 520
- Copyright
- Copyright © Cambridge Philosophical Society 1947
References
REFERENCES
- 9
- Cited by


