No CrossRef data available.
The Symmetric Derivative and its application to the Theory of Trigonometric Series
Published online by Cambridge University Press: 24 October 2008
Extract
1. Let
be a numerical series. If for sufficiently small h > 0 the series
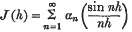
is convergent, we can form the upper and lower limits of J (h) as h → 0. These limits are called respectively the upper and lower sums (R, 1) of the series (1). For the purposes of the present paper it will be convenient to consider a more extended definition of these upper and lower sums. We shall suppose that for sufficiently small h the series J (h) is summable by Poisson's method. We denote the Poisson sum by PJ (h). The upper and lower limits of PJ (h) as h → 0 will be called the upper and lower sums (R, 1) of the series (1).
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 27 , Issue 2 , April 1931 , pp. 163 - 173
- Copyright
- Copyright © Cambridge Philosophical Society 1931
References
† Khintchine, , Fund. Math. 9 (1927), 212–279 (§ 1).CrossRefGoogle Scholar
* Proc. Lond. Math. Soc. 31 (1930), 373.Google Scholar
† Math. Zeit. 25 (1926), 274–290 (Theorem 1, Chap. II).Google Scholar