Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T13:43:41.457Z Has data issue: false hasContentIssue false
  • English
  • Français

The surfaces whose prime-sections contain a

Published online by Cambridge University Press:  24 October 2008

J. Bronowski
J. Bronowski
Affiliation:
Jesus College
Get access Rights & Permissions [Opens in a new window]

Extract

The surfaces whose prime-sections are hyperelliptic curves of genus p have been classified by G. Castelnuovo. If p > 1, they are the surfaces which contain a (rational) pencil of conics, which traces the 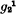on the prime-sections. Thus, if we exclude ruled surfaces, they are rational surfaces. The supernormal surfaces are of order 4p + 4 and lie in space [3p + 5]. The minimum directrix curve to the pencil of conics—that is, the curve of minimum order which meets each conic in one point—may be of any order k, where 0 ≤ k ≤ p + 1. The prime-sections of these surfaces are conveniently represented on the normal rational ruled surfaces, either by quadric sections, or by quadric sections residual to a generator, according as k is even or odd.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 30 , Issue 2 , 30 April 1934 , pp. 170 - 177
Copyright
Copyright © Cambridge Philosophical Society 1934

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Castelnuovo, G., Rend. di Palermo, 4 (1890), 73.CrossRefGoogle Scholar

* If υ is a prime number, then a pencil of elliptic curves of order υ on a rational surface is represented in the plane, either by a pencil R of cubics, or by a Halphen pencil of curves of order 3υ with nine υ-ple base-points (not in general position). In the present case, however, υ = 3, it is easily shown that the Halphen pencil gives rise to surfaces having a unode: they are in fact surfaces discussed by P. Du Val, Proc. London Math. Soc. (2), 35 (1933), 1. Hence the only non-singular surfaces F′ arise from the pencil R of cubics given in the text.

* Bronowski, J., Proc. Camb. Phil. Soc., 29 (1933), 482–3.Google Scholar

† Segre, C., Atti Ace. Torino, 21 (1885), 95.Google Scholar

* Palatini, F., Giorn. di mat., 38 (1900), 315.Google Scholar

* Enriques, F., Rend. Lincei (5), 23 (1914), 206, 291.Google Scholar

* The interesting surfaces F which have b = 1 have been discussed by Val, P. Du, Rend. Lincei (6), 15 (1932), 276.Google Scholar