Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-29T18:23:13.126Z Has data issue: false hasContentIssue false
  • English
  • Français

The summation of Fourier series by logarithmic means

Published online by Cambridge University Press:  24 October 2008

B. Kwee
B. Kwee
Affiliation:
University of Malaya, Kuala Lumpur, Malaysia
Get access Rights & Permissions [Opens in a new window]

Extract

Let {sn} be the sequence of partial sums of the series 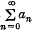and let

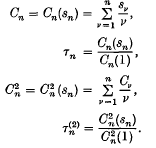
If 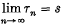, we say that the series is summable (l) to s, and if 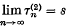, the series is said to be summable (l2) to s. It is clear that .

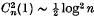Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 70 , Issue 3 , November 1971 , pp. 413 - 419
Copyright
Copyright © Cambridge Philosophical Society 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Borwein, D.A logarithmic method of summability. J. London Math. Soc. 33 (1958), 212–220.CrossRefGoogle Scholar
(2)Hardy, G. H.Divergent series.Google Scholar
(3)Mohanty, R. and Nanda, M.The summability by logarithmic means of the derived Fourier series, Quart. J. Math. (Oxford), Ser. 2, 6 (1955), 53–58.CrossRefGoogle Scholar
(4)Nanda, M.The summability (L) of the Fourier series and the first differentiated Fourier series, Quart. J. Math. Oxford, Ser. 2, 13 (1962), 229–234.CrossRefGoogle Scholar