Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-29T19:06:16.031Z Has data issue: false hasContentIssue false
  • English
  • Français

Summability fields which span the bounded sequences

Published online by Cambridge University Press:  24 October 2008

J. W. Baker  and
G. M. Petersen
J. W. Baker
Affiliation:
University College of Swansea
G. M. Petersen
Affiliation:
University of Canterbury, New Zealand
Get access Rights & Permissions [Opens in a new window]

Extract

If A = (am, n) is a regular matrix, then for any sequence x = {xn}, Am(x) will denote the transform 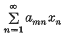and A-lim x denotes 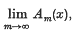if that limit exists. We shall denote by 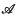the set of bounded sequences which are summed by A. If B is another regular matrix with 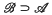then we say that B is b-stronger than A. In that case B must be b-consistent with A (see (4) and (6)), i.e. if 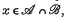then

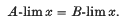
If {μn} is a sequence of positive real numbers with 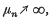we say that A and B are (μn)-consistent if every sequencer x = {xn} satisfying xn = 0(μn) which is summed by both A and B is summed to the same value by both matrices. 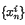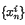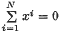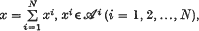A finite set of matrices A1, A2, …, AN is said to be simultaneously (μn)-inconsistent (b-consistent) if whenever is summed by Ai with (i = l, 2, …, N) then implies that The set of sequences, is denoted by

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 63 , Issue 1 , January 1967 , pp. 99 - 106
Copyright
Copyright © Cambridge Philosophical Society 1967

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Baker, J. W. and Petersen, G. M.Inclusion of sets of regular summability matrices. Proc. Cambridge Philos. Soc. 60 (1964), 705–712.Google Scholar
(2)Baker, J. W. and Petersen, G. M.Inclusion of sets of regular summability matrices (II). Proc. Cambridge Philos. Soc. 61 (1965), 381–394.Google Scholar
(3)Baker, J. W. and Petersen, G. M.Inclusion of sets of regular summability matrices (III). Proc. Cambridge Philos. Soc. 62 (1966), 389–394.CrossRefGoogle Scholar
(4)Brudno, A. L.Summation of bounded sequences. Mat. Sbornik. n.s. 16 (1945), 191–247 (in Russian).Google Scholar
(5)Lorentz, G. G. and Zeller, K., Uber paare von Limitierungsverfahren. Math. Z. 68 (1958), 428–438.CrossRefGoogle Scholar
(6)Petersen, G. M.Summability and bounded sequences. Proc. Cambridge Philos. Soc. 55 (1957), 257–261.CrossRefGoogle Scholar
(7)Petersen, G. M.On pairs of summability matrices. Quart. J. Math. Oxford series 16 (1965), 72–76.Google Scholar