Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-29T23:28:50.123Z Has data issue: false hasContentIssue false
  • English
  • Français

Summability factors for Riesz loǵarithmic means of order one for a Fourier series†

Published online by Cambridge University Press:  24 October 2008

R. N. Mohapatra
R. N. Mohapatra
Affiliation:
Regional College of Education, Bhubaneswar, Orissa, India
Get access Rights & Permissions [Opens in a new window]

Extract

Let 0 < λ1 < λ2 < … < λn → ∞ (n→∞). We write

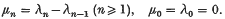
Let ∑an be a given infinite series with the sequence {sn} for its nth partial sum. The (R, λ, 1) mean of the sequence {sn} is given by

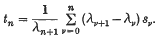
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 67 , Issue 2 , March 1970 , pp. 307 - 320
Copyright
Copyright © Cambridge Philosophical Society 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Andersen, A. F.Studier over Cesàro summabilitets-metode (Copenhagen, 1921).Google Scholar
(2)Bosanquet, L. S.The absolute Cesàro summability of a Fourier series. Proc. London Math. Soc. (2) 41 (1936), 517–528.CrossRefGoogle Scholar
(3)Bosanquet, L. S.Note on Convergence and summability factors (III). Proc. London Math. Soc. (2) 50 (1948), 482–496.CrossRefGoogle Scholar
(4)Bosanquet, L. S.The Cesàro summability of Fourier series and allied series. Proc. London Math. Soc. 37 (1934), 17–32.CrossRefGoogle Scholar
(5)Chow, H. C.Note on convergence and summability factors. J. London Math. Soc. 29 (1954), 459–478.CrossRefGoogle Scholar
(6)Chow, H. C.On the summability factors of a Fourier series. J. London Math. Soc. 16 (1941), 215–220.CrossRefGoogle Scholar
(7)Hardy, O. H. and Littlewood, J. E.Sur la séries de Fourier d'une fonction à carré sommable. C. B. Acad. Sci., Paris, 156 (1913), 1301–1309.Google Scholar
(8)Hardy, G. H. and Littlewood, J. E.The strong summability of Fourier series. Fund. Math. 25 (1935), 162–189.CrossRefGoogle Scholar
(9)Lal, S. N.On the absolute harmonic summability of the factored Fourier series. Proc. Amer. Math. Soc. 14 (1963), 311–319.Google Scholar
(10)Liu, T. S.On the absolute Cesàro summability factors of Fourier series. Proc. Japan Acad. 41 (1965), 757–762.Google Scholar
(11)Moranty, R.On the Summability |R, logω, 1| of a Fourier series. J. London Math. Soc. 25 (1950), 67–72.CrossRefGoogle Scholar
(12)Mohapatra, R. N.Note on summability factors. J. Indian Math. Soc.Google Scholar
(13)Mohapatra, R. N. On absolute Nörlund summability factors (to be published)Google Scholar
(14)Pati, T. and Sinha, S. R.On the absolute summability factors of a Fourier series. Indian J. Math. 1 (1958), 41–54.Google Scholar
(15)Sunouchi, O.Note on Fourier Analysis (XLIV): On the summation of a Fourier series. Tôhoku Math. J. (2), 3 (1951), 114–122.Google Scholar
(16)Sunouchi, G.On the absolute summability factors. Kōdai Math. Sem. Rep. 1 (1954), 59–62.Google Scholar
(17)Szasz, O.Converse theorems of summability for Dirichlet's series. Trans. Amer. Math. Soc. 39 (1936), 117–130.Google Scholar
(18)Zygmund, A.Trigonometrical series (Warsaw, 1935).Google Scholar