Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T14:59:55.805Z Has data issue: false hasContentIssue false
  • English
  • Français

Subexponentially increasing sums of partial quotients in continued fraction expansions

Published online by Cambridge University Press:  17 December 2015

LINGMIN LIAO  and
MICHAŁ RAMS
LINGMIN LIAO
Affiliation:
LAMA UMR 8050, CNRS, Université Paris-Est Créteil, 61 Avenue du Général de Gaulle, 94010 Créteil Cedex, France. e-mail: [email protected]
MICHAŁ RAMS
Affiliation:
Institute of Mathematics, Polish Academy of Sciences, ul. Śniadeckich 8, 00-656 Warszawa, Poland. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

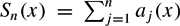We investigate from a multifractal analysis point of view the increasing rate of the sums of partial quotients $S_{n}(x)=\sum_{j=1}^n a_{j}(x)$, where x = [a1(x), a2(x), . . .] is the continued fraction expansion of an irrational x ∈ (0, 1). Precisely, for an increasing function ϕ : 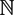$\mathbb{N}$ → 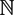$\mathbb{N}$, one is interested in the Hausdorff dimension of the set

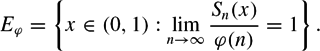E_\varphi = \left\{x\in (0,1): \lim_{n\to\infty} \frac {S_n(x)} {\varphi(n)} =1\right\}.
Several cases are solved by Iommi and Jordan, Wu and Xu, and Xu. We attack the remaining subexponential case exp(nγ), γ ∈ [1/2, 1). We show that when γ ∈ [1/2, 1), Eϕ has Hausdorff dimension 1/2. Thus, surprisingly, the dimension has a jump from 1 to 1/2 at ϕ(n) = exp(n1/2). In a similar way, the distribution of the largest partial quotient is also studied.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 160 , Issue 3 , May 2016 , pp. 401 - 412
Copyright
Copyright © Cambridge Philosophical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Falconer, K.Fractal Geometry, Mathematical Foundations and Application (Wiley, 1990).CrossRefGoogle Scholar
[2]Fan, A. H., Liao, L. M., Wang, B. W. and Wu, J.On Kintchine exponents and Lyapunov exponents of continued fractions. Ergodic Theory Dynam. System 29 (2009), 73–109.Google Scholar
[3]Iommi, G. and Jordan, T.Multifractal analysis of Birkhoff averages for countable Markov maps. Ergodic Theory Dynam. System 35 (2015), 2559–2586.Google Scholar
[4]Jordan, T. and Rams, M.Increasing digit subsystems of infinite iterated function systems. Proc. Amer. Math. Soc. 140 (2012), no. 4, 1267–1279.Google Scholar
[5]Ya, A.Khintchine. Metrische Kettenbruchprobleme. Compositio Math. 1 (1935), 361–382.Google Scholar
[6]Philipp, W.A conjecture of Erdös on continued fractions. Acta Arith. 28 (1975/76), no. 4, 379–386.Google Scholar
[7]Philipp, W.Limit theorems for sums of partial quotients of continued fractions. Monatsh. Math. 105 (1988), 195–206.Google Scholar
[8]Wu, J. and Xu, J.The distribution of the largest digit in continued fraction expansions. Math. Proc. Camb. Phil. Soc. 146 (2009), no. 1, 207–212.Google Scholar
[9]Wu, J. and Xu, J.On the distribution for sums of partial quotients in continued fraction expansions. Nonlinearity 24 (2011), no. 4, 1177–1187.CrossRefGoogle Scholar
[10]Xu, J.On sums of partial quotients in continued fraction expansions. Nonlinearity 21 (2008), no. 9, 2113–2120.Google Scholar