Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-29T23:18:15.571Z Has data issue: false hasContentIssue false
  • English
  • Français

Subdirect products of pro-p groups

Published online by Cambridge University Press:  09 January 2015

DESSISLAVA H. KOCHLOUKOVA  and
PAVEL A. ZALESSKII
DESSISLAVA H. KOCHLOUKOVA
Affiliation:
Department of Mathematics, State University of Campinas (UNICAMP), BrazilRua Sérgio Buarque de Holanda, 651, Campinas, SP, Brasil, CEP 13083-859. e-mail: [email protected]
PAVEL A. ZALESSKII
Affiliation:
Department of Mathematics, University of Brasília, BrazilCampus Universitario, Brasilia-DF, Brasil 70910-900. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study when a pro-p subdirect product S ⩽ G1 × . . . × Gn is of type FPm for m ⩾ 2 for some special pro-p groups Gi. In particular we treat the case when Gi is a finitely generated non-trivial free pro-p product different from C2 ∐ C2 if p = 2 or a non-abelian pro-p group from the class 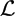$\mathcal{L}$ defined in [12].

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 158 , Issue 2 , March 2015 , pp. 289 - 303
Copyright
Copyright © Cambridge Philosophical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ardakov, K.Krull dimension of Iwasawa algebras. J. Algebra 280 (2004), 190–206.Google Scholar
[2]Bridson, M. R. and Howie, J.Subgroups of direct products of elementarily free groups. Geom. Funct. Anal. 17 (2007), no. 2, 385–403.Google Scholar
[3]Bridson, M. R. and Howie, J.Subgroups of direct products of two limit groups. Math. Res. Lett. 14 (2007), no. 4, 547–558.Google Scholar
[4]Bridson, M. R., Howie, J., Miller, C. F. III and Short, H.Subgroups of direct products of limit groups. Ann. of Math. (2) 170 (2009), no. 3, 1447–1467.Google Scholar
[5]Bridson, M. R., Howie, J., Miller, C. F. III and Short, H.On the finite presentation of subdirect products and the nature of residually free groups. Amer. J. Math. 135 (2013), no. 4, 891–933.Google Scholar
[6]Engler, A., Haran, D., Kochloukova, D. and Zalesskii, P. A.Normal subgroups of profinite groups of finite cohomological dimension. J. London Math. Soc. (2) 69 (2004), no. 2, 317–332.Google Scholar
[7]Farkas, D. R. and Linnell, P. A.Congruence subgroups and the Atiyah conjecture. Groups, rings and algebras, 89102. Contemp. Math. 420 (Amer. Math. Soc., Providence, RI, 2006).Google Scholar
[8]King, J. D.Homological finiteness conditions for pro-p groups. Comm. Algebra 27 (1999), no. 10, 4969–4991.Google Scholar
[9]Kochloukova, D.On subdirect products of type FPm of limit groups. J. Group Theory 13 (2010), no. 1, 1–19.Google Scholar
[10]Kochloukova, D.Subdirect products of free pro-p and Demushkin groups. Intenet. J. Algebra Comput. 23 (2013), no. 5, 1079–1098.Google Scholar
[11]Kochloukova, D. and Short, H.On subdirect product of free pro-p groups and Demushkin groups of infinite depth. J. Algebra 343 (2011), 160–172.Google Scholar
[12]Kochloukova, D. and Zalesskii, P.On pro-p analogues of limit groups via extensions of centralizers. Math. Z. 267 (2011), 109–128.Google Scholar
[13]Kochloukova, D. and Zalesskii, P. On pro-p analogues of limit groups via extensions of centralisers. arXiv 1107.2331.Google Scholar
[14]Kochloukova, D. and Zalesskii, P.Fully residually free pro-p groups. J. Algebra 324 (2010), no. 4, 782–792.Google Scholar
[15]Kochloukova, D. and Zalesskii, P. Subgroups and homology of pro-p extensons of centralizers of pro-p groups. To appear in Math. Nachr.Google Scholar
[16]Kuckuck, B.Subdirect products of groups and the n - (n + 1) - (n + 2) Conjecture. Quart. J. Math. 65 (2014), 1293–1318.Google Scholar
[17]Mel'nikov, O. V.Subgroups and the homology of free products of profinite groups. Math. USSR-Izv. 34 (1990), no. 1, 97–119.Google Scholar
[18]Ribes, L.On amalgamated products of profinite groups. Math. Z. 123 (1971), 357–364.Google Scholar
[19]Ribes, L. and Zalesskii, P.A.Pro-p trees, new horizons in pro-p groups (eds du Sautoy, M, Segal, D. and Shalev, A.). Progr. in Mathe. 184 (Birkhäuser, Boston, 2000).Google Scholar
[20]Snopche, I. and Zalesskii, P.A.Subgroup properties of pro-p extensions of centralisers. Selecta Math. 20 (2014), 465–489.Google Scholar
[21]Zalesskii, P.A.Normal subgroups of free constructions of profinite groups and the congruence kernel in the case of positive characteristic. Izv. Russ. Acad. Sciences, Ser Math. 59 (1995), 499–516.Google Scholar
[22]Zalesskii, P.A. and Melnikov, O.V.Fundamental groups of graphs of profinite groups. Algebra i Analiz 1 (1989); translated in: Leningrad Math. J. 1 (1990) 921–940.Google Scholar
[23]Zapata, T. Grupos pro-finitos limites. PhD. thesis. Universidade de Brasília. (2011).Google Scholar