Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-19T09:41:39.124Z Has data issue: false hasContentIssue false
  • English
  • Français

Statistical mechanics and the partition of numbers II. The form of crystal surfaces

Published online by Cambridge University Press:  24 October 2008

H. N. V. Temperley
H. N. V. Temperley
Affiliation:
King's CollegeCambridge
Get access Rights & Permissions [Opens in a new window]

Abstract

The classical theory of partition of numbers is applied to the problem of determining the equilibrium profile of a simple cubic crystal. It is concluded that it may be thermo-dynamically profitable for the surface to be ‘saw-toothed’ rather than flat, the extra entropy associated with such an arrangement compensating for the additional surface energy. For both a two- and a three-dimensional ‘saw-tooth’ the extra entropy varies, to a first approximation, in the same way as the surface energy, i.e. 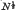is proportional to or 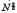respectively, where N is the number of molecules in a ‘tooth’. For the simple cubic lattice, the entropy associated with the formation of a tooth containing N atoms is estimated to be 3.3 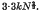It is also possible to estimate the variation of the ‘equilibrium roughness’ of a crystal with temperature, if its surface energy is known.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 48 , Issue 4 , October 1952 , pp. 683 - 697
Copyright
Copyright © Cambridge Philosophical Society 1952

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Auluck, F. C.Proc. Camb. phil. Soc. 47 (1951), 679.CrossRefGoogle Scholar
(2)Auluck, F. C. and Kothari, D. S.Proc. Camb. phil. Soc. 42 (1946), 272.CrossRefGoogle Scholar
(3)Chaundy, T. W.Quart. J. Math. 2 (1931), 234.CrossRefGoogle Scholar
(4)Domb, C. and Potts, R. B.Proc. roy. Soc. A, 210 (1951), 125.Google Scholar
(5)Hardy, G. H.Ramanujan (Cambridge, 1940).Google Scholar
(6)Hardy, G. H. and Ramanujan, S.Proc. Lond. math. Soc. (2), 17 (1918), 75.CrossRefGoogle Scholar
(7)MacMahon, P. A.Combinatory analysis, vol. 2 (Cambridge, 1916).Google Scholar
(8)Onsager, L.Phys. Rev. (2), 65 (1944), 117.CrossRefGoogle Scholar
(9)Temperley, H. N. V.Proc. roy. Soc. A, 199 (1949), 361.Google Scholar
(10)Wright, E. M.Acta math., Stockh., 63 (1934), 143.CrossRefGoogle Scholar