Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T11:22:27.585Z Has data issue: false hasContentIssue false
  • English
  • Français

The squaring operation on -generators of the Dickson algebra†.

Published online by Cambridge University Press:  03 December 2009

NGUYỄN H. V. HƯNG  and
VÕ T. N. QUỲNH
NGUYỄN H. V. HƯNG
Affiliation:
Department of Mathematics, Vietnam National University, Hanoi 334 Nguyễn Trãi Street, Hanoi, Vietnam e-mail: [email protected] e-mail: [email protected]
VÕ T. N. QUỲNH
Affiliation:
Department of Mathematics, Vietnam National University, Hanoi 334 Nguyễn Trãi Street, Hanoi, Vietnam e-mail: [email protected] e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the squaring operation Sq0 on the dual of the minimal -generators of the Dickson algebra. We show that this squaring operation is isomorphic on its image. We also give vanishing results for this operation in some cases. As a consequence, we prove that the Lannes–Zarati homomorphism vanishes (1) on every element in any finite Sq0-family in 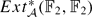except possibly the family initial element, and (2) on almost all known elements in the Ext group. This verifies a part of the algebraic version of the classical conjecture on spherical classes.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 148 , Issue 2 , March 2010 , pp. 267 - 288
Copyright
Copyright © Cambridge Philosophical Society 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Adams, J. F.On the non-existence of elements of Hopf invariant one. Ann. of Math. 72 (1960), 20–104.CrossRefGoogle Scholar
[2]Boardman, J. M.Modular representations on the homology of powers of real projective space, in Algebraic Topology: Oaxtepec 1991. Contemp. Math. 146 (1993), pp. 49–70.Google Scholar
[3]Bousfield, A. K., Curtis, E. B., Kan, D. M., Quillen, D. G., Rector, D. L. and Schlesinger, J. W.The mod p lower central series and the Adams spectral sequence. Topology 5 (1966), 331–342.CrossRefGoogle Scholar
[4]Browder, W.The Kervaire invariant of a framed manifold and its generalization. Ann. of Math. 90 (1969), 157–186.CrossRefGoogle Scholar
[5]Bruner, R. R.The cohomology of the mod 2 Steenrod algebra: A computer calculation. WSU Research Report 37 (1997), 217 pages.Google Scholar
[6]Bruner, R. R., Hà, Lê M. and Hưng, Nguyễn H. V.On behavior of the algebraic transfer. Trans. Amer. Math. Soc. 357 (2005), 473–487 .CrossRefGoogle Scholar
[7]Curtis, E. B.The Dyer–Lashof algebra and the Λ-algebra. Illinois J. Math. 19 (1975), 231–246.CrossRefGoogle Scholar
[8]Dickson, L. E.A fundamental system of invariants of the general modular linear group with a solution of the form problem. Trans. Amer. Math. Soc. 12 (1911), 75–98.CrossRefGoogle Scholar
[9]Giambalvo, V. and Peterson, F. P.-generators for ideals in the Dickson algebra. J. Pure Appl. Algebra 158 (2001), 161–182.CrossRefGoogle Scholar
[10]Goerss, P. G.Unstable projectives and stable Ext: with applications. Proc. London Math. Soc. 53 (1986), 539–561.CrossRefGoogle Scholar
[11]Hà, Lê M.Sub-Hopf algebras of the Steenrod algebra and the Singer transfer. in Proceedings of the School and Conference in Algebraic Topology, 11 (2007), Geom. Topol. Publ. Conventry, pp. 81–105.Google Scholar
[12]Hưng, Nguyễn H. V.Spherical classes and the algebraic transfer. Trans. Amer. Math. Soc. 349 (1997), 3893–3910.Google Scholar
[13]Hưng, Nguyễn H. V.The weak conjecture on spherical classes. Math. Zeit. 231 (1999), 727–743.Google Scholar
[14]Hưng, Nguyễn H. V.Spherical classes and the lambda algebra. Trans. Amer. Math. Soc. 353 (2001), 4447–4460.CrossRefGoogle Scholar
[15]Hưng, Nguyễn H. V.On triviality of Dickson invariants in the homology of the Steenrod algebra. Math. Proc. Camb. Phil. Soc. 134 (2003), 103–113.Google Scholar
[16]Hưng, Nguyễn H. V.The cohomology of the Steenrod algebra and representations of the general linear groups. Trans. Amer. Math. Soc. 357 (2005), 4065–4089.CrossRefGoogle Scholar
[17]Hưng, Nguyễn H. V. and Nam, Trần N.The hit problem for the Dickson algebra. Trans. Amer. Math. Soc. 353 (2001), 5029–5040.Google Scholar
[18]Hưng, Nguyễn H. V. and Peterson, F. P.–generators for the Dickson algebra. Trans. Amer. Math. Soc. 347 (1995), 4687–4728.Google Scholar
[19]Hưng, Nguyễn H. V. and Peterson, F. P.Spherical classes and the Dickson algebra. Math. Proc. Camb. Phil. Soc. 124 (1998), 253–264.Google Scholar
[20]Hưng, Nguyễn H. V. and Quỳnh, Võ T. N.The squaring operation on -generators of the Dickson algebra. Proc. Japan. Acad., Ser. A, 85 (2009), 67–70.Google Scholar
[21]Hưng, Nguyễn H. V. and Quỳnh, Võ T. N. The image of Singer's fourth transfer. C. R. Acad. Sci. Paris, Ser. I (2009), to appear.Google Scholar
[22]Kameko, M. Products of projective spaces as Steenrod modules. Thesis. (Johns Hopkins University 1990).Google Scholar
[23]Lannes, J. and Zarati, S.Sur les foncteurs dérivés de la déstabilisation. Math. Zeit. 194 (1987), 25–59.Google Scholar
[24]Lin, W. H. Some differentials in Adams spectral sequence for spheres. Trans. Amer. Math. Soc., to appear.Google Scholar
[25]Lin, W. H. and Mahowald, M.The Adams spectral sequence for Minami's theorem. in Homotopy theory via algebraic geometry and group representations (Evanston, II., 1997) Contemp. Math. 220 (1998), pp. 143–177.CrossRefGoogle Scholar
[26]Minami, N.The iterated transfer analogue of the new doomsday conjecture. Trans. Amer. Math. Soc. 351 (1999), 2325–2351.Google Scholar
[27]Mùi, HuỳnhModular invariant theory and cohomology algebras of symmetric groups. J. Fac. Sci. Univ. Tokyo, 22 (1975), 310–369.Google Scholar
[28]Nam, Trân N.Transfert algébrique et représentation modulaire du groupe linéare. Ann. Inst. Fourier, 58 (2008), 1785–1837.CrossRefGoogle Scholar
[29]Singer, W. M.Invariant theory and the lambda algebra. Trans. Amer. Math. Soc. 280 (1983), 673–693.CrossRefGoogle Scholar
[30]Singer, W. M.The transfer in homological algebra. Math. Zeit. 202 (1989), 493–523.Google Scholar
[31]Snaith, V. and Tornehave, J.On π*S(BO) and the Arf invariant of framed manifolds. Amer. Math. Soc. Contemp. Math. 12 (1982), 299–313.Google Scholar
[32]Tangora, M. C.On the cohomology of the Steenrod algebra. Math. Zeit. 116 (1970), 18–64.CrossRefGoogle Scholar
[33]Wang, J. S. P.On the cohomology of the mod-2 Steenrod algebra and the non-existence of elements of Hopf invariant one. Illinois J. Math. 11 (1967), 480–490.CrossRefGoogle Scholar
[34]Wellington, R. J.The unstable Adams spectral sequence of free iterated loop spaces. Mem. Amer. Math. Soc. 258 (1982).Google Scholar