Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Davis, Donald M.
Johnson, David C.
Klippenstein, John
Mahowald, Mark
and
Wegmann, Steven
1986.
The spectrum (𝑃∧𝐵𝑃⟨2⟩)_{-∞}.
Transactions of the American Mathematical Society,
Vol. 296,
Issue. 1,
p.
95.
Crabb, M. C.
1991.
On the KOℤ/2-Euler class, II.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 117,
Issue. 1-2,
p.
139.
Greenlees, J. P. C.
and
Sadofsky, Hal
1996.
The Tate spectrum ofv n -periodic complex oriented theories.
Mathematische Zeitschrift,
Vol. 222,
Issue. 3,
p.
391.
Bayen, Dilip
and
Bruner, Robert
1996.
Real connective K-theory and the quaternion group.
Transactions of the American Mathematical Society,
Vol. 348,
Issue. 6,
p.
2201.
Ando, Matthew
Morava, Jack
and
Sadofsky, Hal
1998.
Completions of ℤ∕(p)–Tate cohomology of periodic spectra.
Geometry & Topology,
Vol. 2,
Issue. 1,
p.
145.
Behrens, Mark
2005.
Root invariants in the Adams spectral sequence.
Transactions of the American Mathematical Society,
Vol. 358,
Issue. 10,
p.
4279.
Bailey, Scott M.
and
Ricka, Nicolas
2019.
On the Tate spectrum of
$$\mathrm {tmf}$$
tmf
at the prime 2.
Mathematische Zeitschrift,
Vol. 291,
Issue. 3-4,
p.
821.
Quigley, J D
2019.
The motivic Mahowald invariant.
Algebraic & Geometric Topology,
Vol. 19,
Issue. 5,
p.
2485.
Hu, Po
Kriz, Igor
and
Somberg, Petr
2019.
Tate cohomology of connected k-theory for elementary abelian groups revisited.
Journal of Homotopy and Related Structures,
Vol. 14,
Issue. 3,
p.
749.
Guillou, Bertrand J.
Hill, Michael A.
Isaksen, Daniel C.
and
Ravenel, Douglas Conner
2020.
The cohomology of C2-equivariant 𝒜(1) and the
homotopy of koC2.
Tunisian Journal of Mathematics,
Vol. 2,
Issue. 3,
p.
567.
Quigley, J D
2022.
tmf–based Mahowald invariants.
Algebraic & Geometric Topology,
Vol. 22,
Issue. 4,
p.
1789.
Quigley, J. D.
and
Shah, Jay
2025.
On the parameterized Tate construction.
Journal of Topology,
Vol. 18,
Issue. 1,
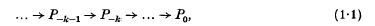
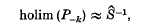
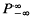 this holim (P–κ), although one must constantly keep in mind that
this holim (P–κ), although one must constantly keep in mind that 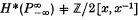 , but rather
, but rather