Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yoshitomi, Kazushi
2009.
Dirac operators with periodic δ-interactions: Spectral gaps and inhomogeneous Diophantine approximation.
Michigan Mathematical Journal,
Vol. 58,
Issue. 2,


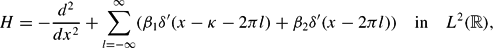
 are parameters. Let τ=2π−κ. Suppose that the ratio κ
are parameters. Let τ=2π−κ. Suppose that the ratio κ