Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-30T21:46:56.140Z Has data issue: false hasContentIssue false
  • English
  • Français

Special values of L-functions and height two formal groups

Published online by Cambridge University Press:  24 October 2008

Rodney I. Yager
Rodney I. Yager
Affiliation:
School of Mathematics, Physics, Computing and Electronics, Macquarie University, N.S.W. 2109, Australia
Get access Rights & Permissions [Opens in a new window]

Extract

Let ψ be the Grossencharacter attached to an elliptic curve E defined over an imaginary quadratic field K ⊂ 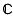of discriminant −dK, and having complex multiplication by the maximal order 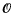of K. We denote the conductor of ψ by 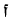and fix a Weierstrass model for E with coefficients in ,

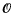whose discriminant 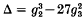is divisible only by primes dividing 6. Let Kab be the abelian closure of K in 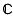and choose a fundamental period Ω ∈ 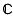for the above model of the curve.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 105 , Issue 1 , January 1989 , pp. 13 - 24
Copyright
Copyright © Cambridge Philosophical Society 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Coleman, R.. Division values in local fields. Invent. Math. 53 (1979), 91–161.CrossRefGoogle Scholar
[2]Dwork, B. M.. On the Tate constant. (To appear.)Google Scholar
[3]Katz, N. M.. Divisibilities, congruences, and Cartier duality. J. Fac. Sci. Univ. Tokyo (Sect. 1A Math.) 28 (1981), 667–678.Google Scholar
[4]Perrin-Riou, B.. Périodes p-adiques. (To appear.)Google Scholar
[5]Robert, G.. Nombres de Hurwitz et unités elliptiques. Thesis, Université de Paris-Sud (1977).Google Scholar
[6]Rubin, K.. Congruences for special values of L-functions of elliptic curves with complex multiplication. Invent. Math. 71 (1983), 339–354.CrossRefGoogle Scholar
[7]Yager, R. I.. p-adic measures on Galois groups. Invent. Math. 76 (1983), 331–343.CrossRefGoogle Scholar