No CrossRef data available.
Article contents
Sparseness for the symmetric hit problem at all primes
Published online by Cambridge University Press: 11 December 2014
Abstract
The hit problem for a module over the Steenrod algebra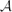 
$\mathcal{A}$ seeks a minimal set of 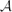$\mathcal{A}$-generators (“non-hit elements,” those not in the image of positive degree elements of 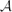$\mathcal{A}$). This problem has been studied for 25 years in a variety of contexts and, although general or complete results have been difficult to obtain, partial results have been obtained in many cases.
For any prime p ⩾ 2, consider the algebra of symmetric polynomials in l variables over 
$\mathbb{F}$p (the cohomology of BU(l) [BO(l) for p = 2]). We prove a general sparseness result: For any l, the 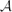$\mathcal{A}$-generators can be concentrated in complex [real for p = 2] degrees τ such that α((p - 1) (τ + l)) ⩽(p - 1)l, where α(m) denotes the sum of the digits in the p-ary expansion of m.
The specialisation of this result to p = 2 was proved by Janfada and Wood using different methods. Key ingredients of our approach are an action of the Kudo–Araki–May algebra on the 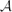$\mathcal{A}$-primitives in homology, and a symmetric homology adaptation of the concept behind the χ-trick in cohomology.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 158 , Issue 2 , March 2015 , pp. 269 - 274
- Copyright
- Copyright © Cambridge Philosophical Society 2014
References
REFERENCES
[1]Alghamdi, M. A., Mohamed, A., Crabb, M. C. and Hubbuck, J. R.Representations of the homology of BV and the Steenrod algebra. I. In Adams Memorial Symposium on Algebraic Topology, 2 (Manchester, 1990) London Math. Soc. Lecture Note Ser., 176 (Cambridge University Press, Cambridge, 1992), pp. 217–234.Google Scholar
[2]Boardman, J. M.Modular representations on the homology of powers of real projective space. In Algebraic Topology (Oaxtepec, 1991) Contemp. Math. 146 (Amer. Math. Soc., Providence, RI, 1993), pp. 49–70.Google Scholar
[3]Chen, S. M. and Shen, X. Y.On the action of Steenrod powers on polynomial algebras, In Algebraic topology (San Feliu de Guíxols, 1990) Lecture Notes in Math. vol. 1509 (Springer, Berlin, 1992), pp. 326–330.Google Scholar
[4]Crossley, M. D.A(p)-annihilated elements in H *(CP(∞) × CP(∞)). Math. Proc. Camb. Phil. Soc.. 120 (1996), no. 3, 441–453.Google Scholar
[5]Crossley, M. D.H*V is of bounded type over 
$\mathcal{A}$(p). In Group Representations: Cohomology, Group Actions and Topology (Seattle, WA, 1996) Proc. Sympos. Pure Math. 63 (Amer. Math. Soc., Providence, RI, 1998), pp. 183–190.Google Scholar
$\mathcal{A}$(p). In Group Representations: Cohomology, Group Actions and Topology (Seattle, WA, 1996) Proc. Sympos. Pure Math. 63 (Amer. Math. Soc., Providence, RI, 1998), pp. 183–190.Google Scholar[6]Crossley, M. D.Monomial bases for H*(CP ∞ × CP ∞) over A(p). Trans. Amer. Math. Soc. 351 (1999), 171–192.Google Scholar
[7]Janfada, A. S. and Wood, R.M.W.The hit problem for symmetric polynomials over the Steenrod algebra. Math. Proc. Camb. Phil. Soc. 133 (2002), 295–303.CrossRefGoogle Scholar
[8]Janfada, A. S. and Wood, R.M.W.Generating H*(BO(3); F 2) as a module over the Steenrod algebra. Math. Proc. Camb. Phil. Soc. 134 (2003), 239–258.CrossRefGoogle Scholar
[9]Kameko, M.Generators of the cohomology of BV 3. J. Math. Kyoto Univ.. 38 (1998), 587–593.Google Scholar
[10]Nam, T. N.$\mathcal{A}$-générateurs génériques pour l'algèbre polynomiale. Adv. Math. 186 (2004), no. 2, 334–362.Google Scholar
$\mathcal{A}$-générateurs génériques pour l'algèbre polynomiale. Adv. Math. 186 (2004), no. 2, 334–362.Google Scholar[11]Pengelley, D. and Williams, F.A new action of the Kudo–Araki–May algebra on the dual of the symmetric algebras, with applications to the hit problem. Algebr. Geom. Topol.. 11 (2011), 1767–1780.Google Scholar
[12]Pengelley, D. and Williams, F.The hit problem for H*(BU(2); $\mathbb{F}$p). Algebr. Geom. Topol.. 13 (2013), 2061–2085.Google Scholar
$\mathbb{F}$p). Algebr. Geom. Topol.. 13 (2013), 2061–2085.Google Scholar[13]Peterson, F. P.A-generators for certain polynomial algebras. Math. Proc. Camb. Phil. Soc.. 105 (1989), 311–312.Google Scholar
[14]Singer, W. M.On the action of Steenrod squares on polynomial algebras. Proc. Amer. Math. Soc.. 111 (1991), 577–583.Google Scholar
[15]Singer, W. M.Rings of symmetric functions as modules over the Steenrod algebra. Algebr. Geom. Topol.. 8 (2008), no. 1, 541–562.Google Scholar
[16]Wood, R. M. W.Steenrod squares of polynomials and the Peterson conjecture. Math. Proc. Camb. Phil. Soc.. 105 (1989), 307–309.Google Scholar