Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T14:16:21.698Z Has data issue: false hasContentIssue false
  • English
  • Français

Some series and integrals involving associated Legendre functions (II)

Published online by Cambridge University Press:  24 October 2008

W. N. Bailey
W. N. Bailey
Affiliation:
Trinity College
Get access Rights & Permissions [Opens in a new window]

Extract

1. In a paper published recently in these Proceedings, I have proved the formulae

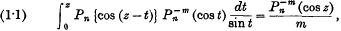
where R(m)>0;

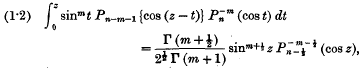
where R(m) > −½; and

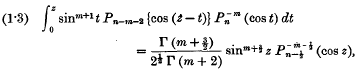
where R(m) >− 1. In each case n is unrestricted.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 27 , Issue 3 , July 1931 , pp. 381 - 386
Copyright
Copyright © Cambridge Philosophical Society 1931

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bailey, W. N., 1; “Some series and integrals involving associated Legendre functions,” Proc. Camb. Phil. Soc. 27 (1931), 184–189.Google Scholar
Bailey, W. N., 2; “Some definite integrals involving Bessel functions,” Proc. London Math. Soc. (2), 31 (1930), 200–208.Google Scholar
Bailey, W. N., 3; “Some integrals of Kapteyn's type involving Bessel functions,” Proc. London Math. Soc. (2), 30 (1930), 422–424.Google Scholar
Van der Pol, B., 1; “On the operational solution of linear differential equations and an investigation of the properties of these solutions,” Phil. Mag. 8 (1929), 861–898.Google Scholar
Watson, G. N., 1; Theory of Bessel Functions.Google Scholar